土壤和地下水中的挥发性(VOCs)或半挥发性(SVOCs)的有机污染物，可以经由扩散、对流和吸附等过程通过土壤传播至建筑物地基，再通过建筑物墙体上的裂缝(或缺口)进入室内影响室内空气质量，进而对人体产生潜在的健康危害，这一过程被称之为“蒸气入侵”(vapor intrusion, VI)[1]。由于国内大部分污染场地属搬迁场地(棕色地块)，无法通过测量建筑物室内空气或建筑物地基处污染物的浓度进而判断VI风险，美国环境保护局(US EPA)发布的VI指南[2]建议可以通过数学模型识别潜在的VI风险，特别针对“棕色地块”重建的情况，通过数学模型预测VI过程引起的风险已经非常普遍[3]。其中最为典型的是Johnson-Ettinger(1991)模型[4](下文简称J-E模型)。
相关研究显示，J-E模型预测的结果过于保守。芦伟等[5]通过箱体试验评估J-E模型，模型预测的室内污染物浓度值大于试验检测值，相对偏差在14.0%～31.9%。Hers等[6]的研究结果同样显示J-E模型预测结果比实测值高2个数量级。此外对US EPA的VI数据库的研究表明[7-8]，土壤蒸气在污染源-室内过程中浓度衰减高达6～7个数量级，而通过J-E模型预测，计算得到室内污染物浓度衰减因子仅有3～5个数量级。J-E模型作为US EPA推荐适用模型也收录于我国《建设用地土壤污染风险评估技术导则》[9](HJ 25.3—2019)中，广范应用于场地蒸气入侵风险评估中。通过模型预测风险过于保守时，会放大VOCs或SVOCs污染场地的健康风险评估结果，进而增加场地修复的成本和时间。合理的模型结构和针对应用场景的模型参数是提高模型预测准确性的2个重要部分，更好地优化模型成为精确评估风险必然的研究方向。雷城英等[10]根据研究的场地和污染物特征，修正了C-RAG模型3项首要参数，基于修正后的模型评估的致癌风险水平普遍降低了一个量级。Hers等[11]的研究表明J-E模型预测结果严重依赖于参数，但目前对于优化J-E模型参数的研究较少。Johnston等[12]曾通过贝叶斯反演方法优化模型输入参数，更新后的模型将预测浓度的均方根误差降低了66%。但该方法计算量大，且需在掌握实测室内污染物浓度(已知风险)的前提下进行优化，不适用于实际应用过程中蒸气入侵风险的评估。本研究结合敏感性分析结果对J-E模型参数进行修正、并利用三维数值模型检验修正效果，以期提高模型预测精确度，为管控场地蒸气入侵风险提出新的思路。
1 J-E模型概述(J-E model overview)
J-E模型[4]是被广泛使用的用于估计场地VI风险的一维(1-D)筛选模型，其表达式为：
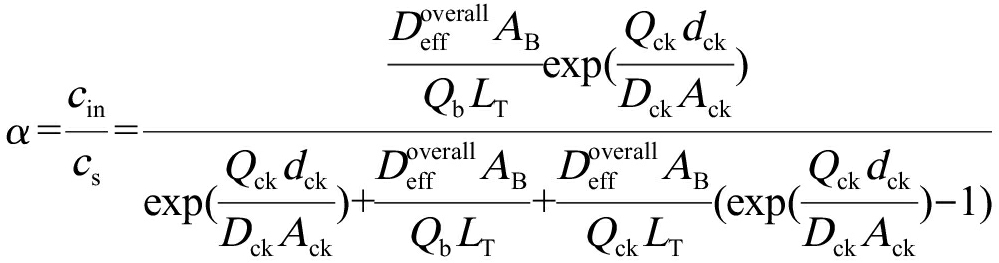
(1)
式中：α为污染源-室内污染物浓度的衰减因子，cin为室内污染物浓度(mg·m-3)；cs为污染源浓度
为污染物在土壤中总有效扩散系数(m2·s-1)；LT为污染源到建筑物地基的距离(m)；AB为污染物气体通过建筑物地基的表面积(m2)；Qb为建筑物通风率(m3·s-1)；Qck为土壤气体进入建筑物的体积流速(m3·s-1)；dck为建筑物地基厚度(m)；Dck为污染物在缝隙中的扩散速率(m2·s-1)；Ack为缝隙面积(m2)；当污染源为地下水时，由于土壤毛细管层作用的影响，污染物在土壤中的总有效扩散系数
计算方式为：
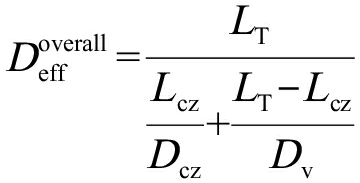
(2)
式中：Lcz为毛细管层厚度(m)；Dv为污染物在土壤气相中的有效扩散系数(m2·s-1)；Dcz为污染物在毛细管层中的有效扩散系数(m2·s-1)；而Dcz可以通过Millington-Quirk方程计算。污染物在毛细管层中的水分含量可以根据US EPA以J-E模型为基础编制的电子表格中提供的参数结合Van Genuchten方程估计：
(3)
式中：θw,cz为毛细管层含水率；θt为土壤饱和含水率；θr为土壤残余含水率；N为曲线形状参数；M=1-1/N；Hc为压力水头(m)；β为土壤水分特征曲线参数(cm-1)。
毛细管层的厚度则通过经验公式估算：
(4)
式中：σ为水的表面张力系数(g·s-2)；λ为毛细管液面与毛细管壁的接触角，默认为0；ρw为水的密度(g·cm-3)；g为重力加速度(m·s-2)；D为平均粒径(cm)。
2 研究方法(Methods)
采用以下方法对J-E模型参数进行敏感性分析[13]：
(5)
式中：x是目标参数，在J-E模型中选取地基厚度(dck)、污染源深度(ds)、毛细管层厚度(Lcz)、非饱和层含水率(θw,ncz)、毛细管层含水率(θw,cz)、封闭空间体积(Vb)和空气交换速率(Ae)；Δ是目标函数变化范围，这里选取基于已定基准相应增加或减少10%；φ是除了目标参数以外的J-E模型默认参数；f指J-E模型。
通过以上方法，计算基于目标参数变化后的污染物浓度衰减因子的变化，进而判断模型敏感参数。
基于以上分析结果，对J-E模型参数进行修正，并计算参数修正后的浓度衰减因子(α)，与三维数值模型(the Brown model，Comsol Multiphysics)模拟结果进行比较。三维数值模型设置参数如表1所示。
3 研究结果(Results)
3.1 敏感性分析
敏感性分析结果如图1所示，图中Y轴为J-E模型中的主要参数(土壤质地选用壤土)，X轴为基于已给定参数为基准相应地增加或减少10%，获得的污染物浓度衰减因子的变化。由图1可知，θw,cz对J-E模型的预测值影响最大，其次是Ae、Vb和Lcz。
3.2 参数修正
根据US EPA提供的J-E模型电子表格中12种不同土壤质地参数分别利用J-E模型和三维数值模拟计算污染物浓度衰减因子，结果如图2和图3所示。由图可知，通过J-E模型预测的污染物浓度衰减因子普遍要比3-D数值模型高1～2个数量级。US EPA电子表格参数如表2所示。
表1 三维数值模拟使用参数
Table 1 Parameters of 3-D numerical simulations
参数Parameter符号Symbol单位Unit数值Value数据来源Reference压力差 Indoor depressurizationΔpPa-5[14]污染源深度 Source depthdsm2.2, 6.2,4, 8[14]建筑物地基长 Foundation footprint lengthm10[14]建筑物地基宽 Foundation footprint widthm10[14]建筑物地基深 Foundation depthdfm0.2, 2[14]封闭空间体积 Volume of the enclosed spaceVbm3366[15]空气交换速率 Air exchange rateAeh-10.45[15]建筑物地基厚度 Foundation crack thicknessdckm0.15[14]建筑物地基裂缝宽 Foundation crack widthwckm0.001[16]分配系数 Partition coefficientKaw空气中有效扩散系数 Diffusion coefficient in airDgm2·s-1水中有效扩散系数 Diffusion coefficient in waterDwm2·s-1
图1 污染源-室内过程J-E模型污染物浓度衰减因子使用参数敏感性分析(土壤选用壤土)
Fig. 1 Sensitivity analysis of parameters on source-to-indoor air concentration attenuation factors of J-E model (the soil type is loam)
结合敏感性分析结果，对J-E模型的修正有必要将毛细管层的水分含量考虑进去。本文对土壤毛细管中水分含量选取的是US EPA提供的J-E模型电子表格中不同质地土壤的饱和含水率，将新的毛细管层中土壤水分含量带入J-E模型，结果如图2和图3所示，发现此种情况下的J-E模型的预测值与三维数值模拟仍相差约1个数量级。
Shen等[17]的研究表明，J-E模型中土壤毛细管层厚度的计算方法可能并不能恰当地表征水分在土壤中的分布，土壤中水分的含量与毛细管压头有关，这一性质又与水的表面张力有关：
(6)
所以Shen等[17]建议土壤毛细管层厚度可以通过Dexter和Bird[18]提供的方法，即毛细管层的高度等于VG方程描述的水分特征曲线拐点处的毛细管压头(以土壤水分含量的对数值作图)则：
(7)
式中：M为与曲线形状参数相关的参数。稳态下，土壤中气相的压力与水相压力相比较小，可忽略不计，则：
(8)
式中：Hc为毛细管压头(m)；pg为气相压力(Pa)；pw为水相压力(Pa)；ρw为水相密度(g·cm-3)；g为重力加速度(m·s-2)。
将获得的新的毛细管层厚度带入J-E模型中，得到的污染物浓度衰减因子如图2和图3所示，由图可知，根据Shen等[17]的建议对毛细管层厚度的修正并不会使污染物浓度衰减因子发生显著的变化，与修正毛细管层含水量方法结果差距不是很明显，尤其是在地板暴露场景下。
针对以上2种分析方法，可以考虑同时修正毛细管层中水分含量及其高度，结果如图2和图3所示。修正后的J-E模型预测结果与三维数值模型的计算结果较为吻合，两者的差距不到1个数量级。且对于地板(图2)和地下室(图3)不同暴露场景，地基较深的场景(图3)修正模型预测效果更好。
4 讨论(Discussion)
为消除J-E模型预测结果过于保守的现象，提高模型预测准确性。敏感性分析方法作为确定模型重要参数的科学方法，被应用到本研究中。对J-E模型敏感性分析结果显示，毛细管层中土壤的水分含量以及毛细管层厚度是影响模型预测精确度的重要参数。
研究提出，采用US EPA推荐的饱和含水量对将毛细管层土壤水分含量进行修正，毛细管层厚度采用VG方程描述的水分特征曲线拐点处的毛细管压头进行修正。两者相结合后，模型的预测结果与三维数值模拟的结果从相差2个数量级到几乎等于三维模拟结果，也更接近US EPA的VI数据库真实数据值，提高了模型预测的精确度，更加适用于蒸气入侵风险评估工作。
表2 J-E模型电子表格中Van Genuchten方程参数
Table 2 The Van Genuchten parameters in J-E model spreadsheet
土壤质地Soil texture typeβNθtθrκ平均粒径/mmMean grain diameter/mm粉质粘土 Silty clay1.6221.3210.4810.1111.48E-133.90E-02粉砂土 Silt0.6581.6790.4890.0506.74E-134.60E-02粉质粘土壤 Silty clay loam0.8391.5210.4820.0901.70E-135.60E-02粘土 Clay1.4961.2530.4590.0982.26E-139.20E-02粉质壤土 Silty loam0.5061.6630.4390.0652.82E-131.10E-01粘质壤土 Clay loam1.5811.4160.4420.0791.26E-131.60E-01壤土 Loam1.1121.4720.3990.0611.85E-132.00E-01砂质粘土 Sandy clay3.3421.2080.3850.1171.74E-132.50E-01砂质粘壤土 Sandy clay loam2.1091.3300.3840.0632.04E-132.90E-01砂质壤土 Sandy loam2.6671.4490.3870.0395.93E-133.00E-01壤质砂土 Loam sand3.4751.7460.3900.0491.62E-124.00E-01砂土 Sand3.5243.1770.3750.0539.92E-124.40E-01
注：β和N为土壤水分曲线参数；θt为土壤饱和含水率；θr为土壤残余含水率；κ为渗透系数(m·s-1)。
Note: β and N are soil moisture curve parameters; θt is soil saturated water content; θr is soil residual water content; κ is soil hydraulic conductivity (m·s-1).
图2 风险筛选模型和数值模型关于不同质地土壤污染源-室内污染物浓度衰减因子的比较(地板暴露场景)
Fig. 2 Comparison of source-to-indoor air concentration attenuation factors between screening models
and numerical results for slab-on-grade scenario
图3 风险筛选模型和数值模型关于不同质地土壤污染源-室内污染物浓度衰减因子的比较(地下室暴露场景)
Fig. 3 Comparison of source-to-indoor air concentration attenuation factors between screening models
and numerical results for basement scenarios
研究提供了提高模型预测精确度的一种方法，但由于其模型参数较多，预测结果的不确定性依然存在。Moradi等[19]基于Sobol指数的全局敏感性分析技术来评估J-E模型对输入参数变化的敏感性。其结果表明，空气交换速率和有效扩散系数也是影响模型预测结果的重要参数，但在本研究中未将这2种参数的不确定性考虑进去。其次，黄凤莲等[20]根据我国居住用地的特点对J-E模型参数进行本地化修正，并于实际场景中对比修正前后的模型预测结果，修正后的模型预测风险显著降低。本研究验证修证模型准确度采用US EPA推荐参数。如室内外压强差为-5 Pa，而在我国《建设用地土壤污染风险评估技术导则》(HJ25.3—2019)中推荐值为0，其次我国目前不考虑土壤质地情况，毛细管层厚度推荐值为5 cm(HJ25.3—2019)，而US EPA提出针对不同土壤质地采用不同厚度值进行计算。因此实际预测过程中，由于场景千差万别，在应用J-E模型评估风险时，为更加精确评估风险，应尽可能多的获取较准确的参数输入值。
通讯作者简介：尧一骏(1984—)，男，博士，研究员，主要研究方向为污染场地的风险评估与治理。
[1] U.S. Environmental Protection Agency (US EPA). What is vapor intrusion [EB/OL]. (2012-01-01) [2021-07-01]. https://www.epa.gov/vaporintrusion/what-vapor-intrusion
[2] U.S. Environmental Protection Agency (US EPA). Technical guide for assessing and mitigating the vapor intrusion pathway from subsurface vapor source to indoor (OSWER) [R]. Washington DC: US EPA, 2015
[3] ASTM. Standard guide for risk based corrective action applied at petroleum release sites [S]. Washington,D,C: American Society of Testing Materials 1995
[4] Johnson P C, Ettinger R A. Heuristic model for predicting the intrusion rate of contaminant vapors into buildings [J]. Environmental Science & Technology, 1991, 25(8): 1445-1452
[5] 芦伟, 李忠元, 杨洁, 等. 箱体实验验证Johnson & Ettinger蒸气入侵模型[J]. 华东理工大学学报:自然科学版, 2018, 44(3): 382-389
Lu W, Li Z Y, Yang J, et al. Experimental validation of Johnson & Ettinger vapor intrusion model with a scale model [J]. Journal of East China University of Science and Technology: Natural Science Edition, 2018, 44(3): 382-389 (in Chinese)
[6] Hers I, Zapf-Gilje R, Johnson P C, et al. Evaluation of the Johnson and Ettinger model for prediction of indoor air quality [J]. Groundwater Monitoring & Remediation, 2003, 23(2): 119-133
[7] Yao Y J, Shen R, Pennel K G, et al. A numerical investigation of oxygen concentration dependence on biodegradation rate laws in vapor intrusion [J]. Environmental Science Processes & Impacts, 2013, 15(12): 2345-2354
[8] Yao Y J, Pennell K G, Surberg E M. Simulating the effect of slab features on vapor intrusion of crack entry [J]. Building and Environment, 2013, 59: 417-425
[9] 中华人民共和国生态环境部. 建设用地土壤污染风险评估技术导则: HJ25.3—2019[S]. 北京: 中华人民共和国生态环境部, 2019
[10] 雷城英, 李玉进, 王梦珂, 等. C-RAG模型在砷污染场地中的修正及应用研究[J]. 生态毒理学报, 2021, 16(1): 147-154
Lei C Y, Li Y J, Wang M K, et al. Research on modification and application of C-RAG model in arsenic contaminated site [J]. Asian Journal of Ecotoxicology, 2021, 16(1): 147-154 (in Chinese)
[11] Hers I, Zapf-Gilje R, Evans D, et al. Comparison, validation, and use of models for predicting indoor air quality from soil and groundwater contamination [J]. Soil and Sediment Contamination: An International Journal, 2002, 11(4): 491-527
[12] Johnston J E, Sun Q, Gibson J M. Updating exposure models of indoor air pollution due to vapor intrusion: Bayesian calibration of the Johnson-Ettinger model [J]. Environmental Science & Technology, 2014, 48(4): 2130-2138
[13] Clewell R A, Merrill E A, Yu K O, et al. Predicting fetal perchlorate dose and inhibition of iodide kinetics during gestation: A physiologically-based pharmacokinetic analysis of perchlorate and iodide kinetics in the rat [J]. Toxicological Sciences, 2003, 73(2): 235-255
[14] Abreu L D V, Johnson P C. Effect of vapor source-building separation and building construction on soil vapor intrusion as studied with a three-dimensional numerical model [J]. Environmental Science & Technology, 2005, 39(12): 4550-4561
[15] U.S. Environmental Protection Agency (US EPA). Documentation for EPA’s implementation of the Johnson and Ettinger model to evaluate site specific vapor intrusion into buildings [S]. Washington DC: US EPA, 2017
[16] Yao Y J, Shen R, Pennell K G, et al. Comparison of the Johnson-Ettinger vapor intrusion screening model predictions with full three-dimensional model results [J]. Environmental Science & Technology, 2011, 45(6): 2227-2235
[17] Shen R, Pennell K G, Surberg E M. Influence of soil moisture on soil gas vapor concentration for vapor intrusion [J]. Environmental Engineering Science, 2013, 30(10): 628-637
[18] Dexter A R, Bird N R A. Methods for predicting the optimum and the range of soil water contents for tillage based on the water retention curve [J]. Soil and Tillage Research, 2001, 57(4): 203-212
[19] Moradi A, Tootkaboni M, Pennell K G. A variance decomposition approach to uncertainty quantification and sensitivity analysis of the Johnson and Ettinger model [J]. Journal of the Air & Waste Management Association, 2015, 65(2): 154-164
[20] 黄凤莲, 杜红花, 陈跃辉, 等. 基于居住用地规划室内蒸汽入侵模型修正的污染场地健康风险评估应用研究[J]. 湘潭大学学报: 自然科学版, 2020, 42(1): 76-85
Huang F L, Du H H, Chen Y H, et al. Health risk assessment of contaminated sites based on modification of indoor vapor invasion model in residential land planning [J]. Journal of Xiangtan University: Natural Science Edition, 2020, 42(1): 76-85 (in Chinese)