在环境中,重金属是指有毒金属(例如,镉(Cd)、铅(Pb)、铬(Cr)、银(Ag)、锡(Sn)和汞(Hg))或限制性营养元素(例如,铁(Fe)、锰(Mn)、铜(Cu)、锌(Zn)、钼(Mo)、钴(Co)和镍(Ni))。有毒金属可通过营养元素的运输系统进入生物体,进一步取代营养元素的活性代谢位点[1-3]。水体环境中的重金属总量可以反映水体环境所受污染程度,但是并不能作为一个很好的指标来反映重金属的生物有效性以及对水生生物所产生的直接效应。因此,研究重金属的生物有效性也是科学制定基准的前提和有力保障。美国环境保护局(US EPA)运用生物配体模型(biotic ligand model, BLM)建立Cu的水环境质量基准(water quality criteria, WQC;简称水质基准)[4]。在我国,虽然已经有了基于水体中重金属总浓度的WQC,但是用生物有效性模型确定中国水体的WQC迫在眉睫,复杂多变的水环境因子对重金属毒性的影响会影响水质基准的制定[5]。
目前,2个主要的生物有效性模型用于定量评估水环境中金属的毒性:BLM考虑了物种特征(即BL泛指生物膜上的受体),并提供了一个用于确定水化学条件对金属毒性影响的框架[6]。BLM认为金属生物毒性取决于结合到生物膜BL上的金属的浓度,以及溶液中某些阳离子(例如H+、K+、Na+、Ca2+及Mg2+)的浓度[6]。这些阳离子可能与金属离子竞争性结合BL的位点[4]。当结合到生物膜BL上的金属的积累量超过临界浓度时,就会发生毒性作用[5]。BLM关注某一暴露终点的毒性效应。相比之下,毒代动力学-毒效动力学(toxicokinetic-toxicodynamic, TK-TD)模型可以模拟有毒金属对生物产生毒性的时间过程[7]。TK模型描述以溶液中金属浓度为函数的体内的金属浓度随时间的变化过程。简化的TK模型包括金属的吸收和排出过程,但精细化TK模型除了包括金属的吸收和排出过程,还可包括在靶器官或靶部位金属浓度的变化(即体内分布或生物代谢)。TD模型可定量地描述体内金属浓度在生物靶部位产生的毒性效应(如死亡率(mortality)、生理损伤(damage)等)随时间的变化过程[7]。认识到BLM无法实时地模拟金属积累及产生毒性的过程[6],也认识到TK-TD模型中的参数没有考虑水化学条件(如H+)对金属毒性的影响。因此,需要建立既考虑水化学条件又考虑时间过程的TK-TD模型去实时地模拟金属的生物蓄积性及产生的毒性。TK模型模拟金属的生物累积过程,而用TD模型描述与金属累积相对应所产生的毒性[7]。BLM中金属吸收速率是关于水化学参数和阳离子与配体络合常数的函数关系式[8]。将BLM推导出金属的吸收速率引入TK-TD模型中,扩大模型在特定水化学条件下的应用范围。此外,阳离子(如H+、K+、Na+、Ca2+及Mg2+)对非必需金属(Cd和Pb)的毒性影响没有一致的结论,有研究指出K+、Na+、Ca2+及Mg2+对Cd对虹鳟鱼(Oncorhynchus mykiss)的毒性没有影响[9],而K+、Na+、Ca2+及Mg2+浓度升高对Cd对大型溞(Daphnia magna)的毒性具有抑制作用[10]。然而,H+对非必需金属(Cd和Pb)的毒性影响有一致的结论,H+浓度升高对Cd对大型溞(Daphnia magna)的毒性具有抑制作用[10]。因此,本研究中初步开发了基于氢离子与配体(BL)络合常数的TK-TD模型去预测在不同pH条件下非必需金属(Cd和Pb)短期染毒在斑马鱼幼鱼体内的积累及产生的毒性,并评估模型的准确性。
1 模型构建与实施(Model construction and implementation)
1.1 生物配体模型(BLM)
BLM通过Cd2+或Pb2+与BL的络合常数,即KCdBL和KPbBL(L·mol-1),描述Cd2+或Pb2+与BL络合能力[6]。并且假设KCdBL和KPbBL在不同的水化学(如H+)条件下是恒定不变的,KCdBL或KPbBL表示为:
或
(1)
式中:cCd2+和cPb2+是没有结合BL的自由的Cd2+或Pb2+的浓度(mol·L-1);cCdBL或cPbBL表示与BL结合的Cd2+或Pb2+的浓度(mol·L-1);cBL表示没有结合任何阳离子的自由的BL浓度(mol·L-1)。
BLM中毒性是关于结合Cd2+或Pb2+的配体位点浓度cCdBL或cPbBL占总的配体位点浓度(cBL-T)比例系数(fCdBL或fPbBL)的剂量-效应函数[6]。本研究中以H+为例,考虑Cd2+或Pb2+和H+之间的竞争,fCdBL或fPbBL是由KCdBL、KPbBL、KHBL、cCd2+、cPb2+和cH+组成的函数。fMBL计算如下:
(2)
1.2 毒代-毒效动力学(TK-TD)模型
本研究中,TK模型只考虑鱼对金属的吸收和排出过程,忽略金属在鱼体内的生物代谢过程。溶液中Cd2+或Pb2+的浓度,即cCd2+或cPb2+,作为模型的输入变量来模拟随着时间的变化鱼体内Cd或Pb浓度。TD模型描述随着时间的变化鱼体内Cd或Pb浓度和在个体水平上产生的毒性效应(死亡率)量效关系。本研究采用基于配体络合常数KCdBL或KPbBL的TK-TD模型来预测斑马鱼幼鱼体内的金属浓度及产生的毒性随时间变化过程(图1)。实验期间不喂食,在TK模型的质量平衡微分方程中只考虑幼鱼通过呼吸作用(口和鳃)摄取的金属[11-12]。
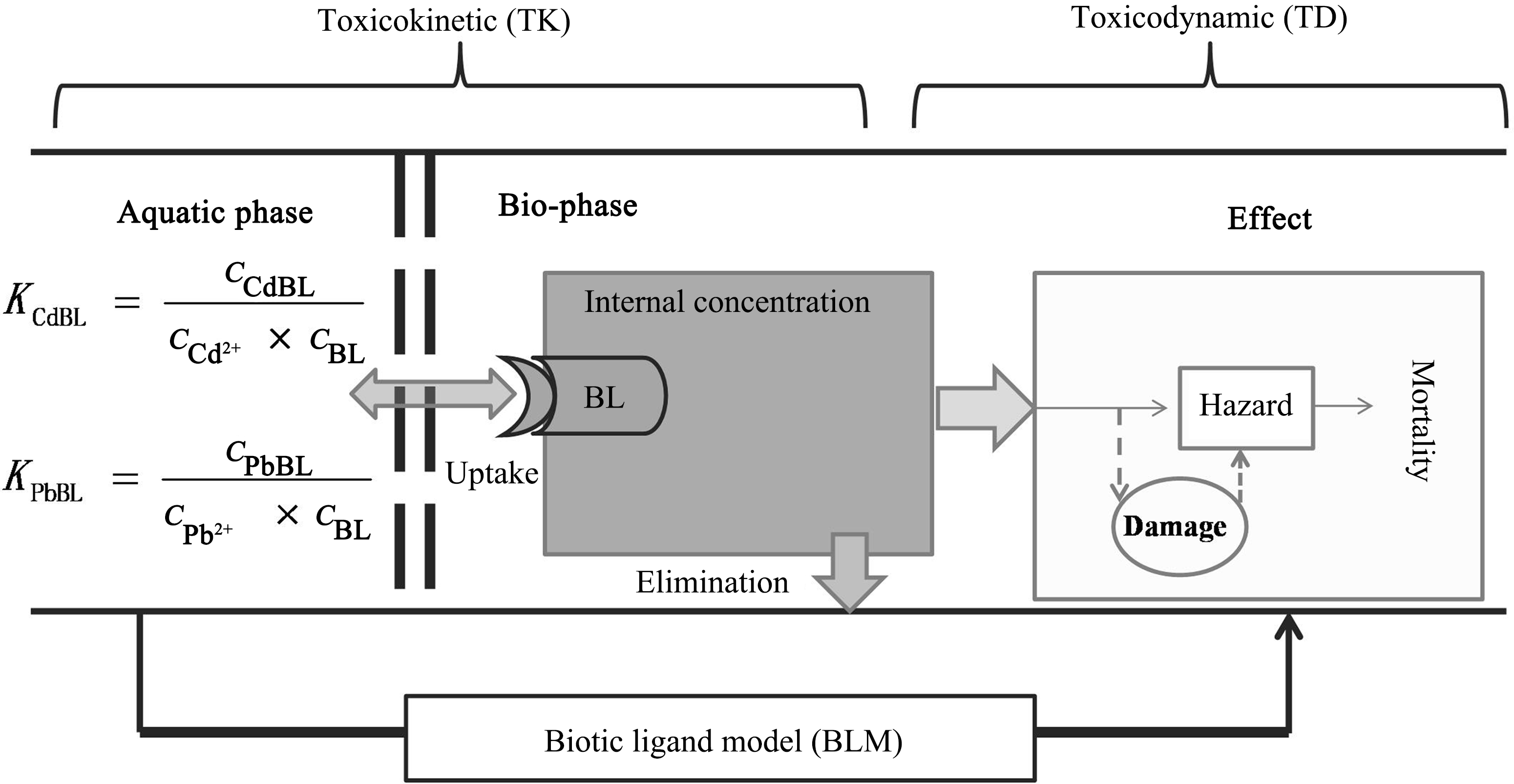
图1 TK-TD模型构成
注:各个符号的意义见正文中式(1)～(8)的说明。
Fig. 1 The re
ned TK-TD model
Note: For the meaning of symbols see the explanation for Eqs. (1)～(8) in the context.
1.2.1 TK模型
本研究中,短期实验期间不喂食幼鱼,不考虑通过食物相进入鱼体内的金属,只考虑水相中金属的吸收。研究Cd或Pb随着时间的增加在鱼体内积累TK模型的基本假设包括[13-14]:(1)只考虑进入生物体内的Cd或Pb(通过洗脱去除可逆地吸附在生物膜表面上的BL位点上的Cd2+或Pb2+的干扰)。(2)Cd或Pb的吸收是主动运输过程,通常由米氏动力学方程描述,即是Cd或Pb最大吸收速率(JCd,max或JPb,max,μg·g-1·h-1)、金属吸收的米氏常数或金属在传输位点上的半饱和常数(Km,Cd或Km,Pb,mol·L-1)和染毒溶液中cCd2+或cPb2+(mol·L-1)的函数[13]。Cd或Pb以被动扩散的形式由鱼体内排出体外,并且是特定物种的金属的排出速率常数(kCd,out或kPb,out,h-1)以及体内金属浓度(CCd,int或CPb,int,μg·g-1)的函数。
因此,Cd或Pb鱼体内积累过程可以表示为[13-14]:
(3)
(4)
式中:t为染毒时间(h);α为幼鱼初始质量(g);β为幼鱼生长速率(g·h-1)。本研究短期毒性试验中,没有喂食时,斑马鱼幼鱼的生长可以忽略不计,β被设为零。
通过KCdBL和Km,Cd之间的倒数关系将络合常数KCdBL引入到TK模型中[15],且KCdBL和KHBL是物种特征参数,不同物种参数值不同。本研究中以H+为例,考虑金属离子和H+之间的竞争,随着时间的增加,Cd在鱼体内的积累是由JCd,max、KCdBL、KHBL、cH+和cCd2+组成的函数。引入到TK模型中,式(3)可以改写为:
(5)
1.2.2 TD模型
TD模型确定生物存活率与体内金属浓度之间量效关系[13-14],微分方程用于模拟随时间的变化,Cd或Pb体内浓度的变化引起的生物存活率的变化,如式(6)～(8)。该模型假设所有幼鱼毒性敏感性是相同的,死亡是一个随机过程[16]。死亡风险率(H(t),量纲为1)是Cd或Pb在鱼体内开始积累到浓度超过一定安全阈值(threshold,μg·g-1)时,增加幼鱼死亡的概率[13-14],以Cd为例,表示为:
=kk×max[CCd,int(t)-threshold,0]
(6)
S(t)=e-H(t)×Scontrol(t)
(7)
Scontrol(t)=e-hb×t
(8)
式中:S(t)是t时刻时,生物的存活率(量纲为1),kk是致死速率常数(g·μg-1·h-1),表示超过安全阈值每单位金属浓度的致死速率,threshold是不引起生物死亡时,体内允许的最高金属浓度(μg·g-1);Scontrol(t)是对照组中生物的存活率(量纲为1),hb是对照组的风险率(h-1)。在本研究中,hb被设为零,因为在Cd或Pb毒性试验期间(≤96 h)对照组幼鱼没有死亡。
2 材料与方法(Materials and methods)
2.1 化学试剂
在超纯水(Milli-Q,18.2 MΩ·cm)中分别加入氯化镉(CdCl2·2.5H2O)和硝酸铅(Pb(NO3)2)(>99%,优级纯,科密欧)配制Cd或Pb储备液。再用超纯水将储备液稀释成一系列浓度的Cd和Pb的染毒溶液。通过加入稀HCl(0.012 mol·L-1)(>99%,优级纯,科密欧)调节染毒溶液的pH。
2.2 模式生物
斑马鱼(Danio rerio,AB系)购自中国科学院水生生物研究所(武汉),饲养于20 L水族玻璃缸[17],水温保持在(26±0.5) ℃,保持12 h光照和12 h黑暗的光周期。每天用薄片高蛋白鱼饲料喂食2次。将斑马鱼雌鱼和雄鱼按2∶1配对,自然交配产卵,采用虹吸法收集胚胎并用清水冲洗干净。
2.3 染毒实验
斑马鱼胚胎发育72 h后完全孵化(胚胎一般从54 h后开始孵化)出的幼鱼用于染毒实验。所有幼鱼染毒实验水温控制(26±0.5) ℃,光照/黑暗周期控制在12 h/12 h,并在无菌六孔细胞培养板中进行染毒(Cellstar,Greiner Bio-one,德国),每孔10 mL测试溶液,每孔30条幼鱼。在六孔细胞培养板的表面上覆盖保鲜膜,防止染毒溶液过量的蒸发导致溶液中金属浓度的变化。
2.3.1 H+与BL络合常数(KHBL)的测定
在pH范围为4.5～7测试体系中评估Cd或Pb的毒性,同时保持其他测试条件不变的情况下来确定的。根据预实验浓度分别确定0～5 mg·L-1 Cd和0～10 mg·L-1 Pb的浓度变化范围,使用超纯水稀释Cd或Pb储备液来获得测试溶液,用HCl(0.012 mol·L-1)调节各测试溶液的pH,并使用pH计(S20P-K SevenEasy Plus,Mettler Toledo,瑞士)测定。染毒溶液各pH体系中,每个金属浓度设置3个平行,染毒24 h后记录幼鱼死亡率。
2.3.2 金属的吸收速率(JCd,int和JPb,int)和排出速率(kCd,out和kPb,out)、致死速率常数(kk)和阈值(threshold)的测定实验
使用pH 7.0左右的超纯水分别设置0.1 mg·L-1 Cd和1 mg·L-1 Pb进行金属在幼鱼体内的积累和毒性实验。实验中选择9个时间点(4、8、12、18、24、36、48、72和96 h)作为采样时间。在每次更新染毒溶液之前测定溶液的pH值,每天更新相应pH值的染毒溶液。收集染毒初始时刻和染毒溶液更新之前的溶液各5 mL,每个浓度制备2个平行样待测浓度。
2.3.3 金属在生物体内积累和毒性验证实验
染毒溶液不同pH条件下(pH为4.5、5.5和6.5),分别设置0.1 mg·L-1 Cd和1 mg·L-1 Pb进行金属在幼鱼体内的积累和毒性实验。实验中选择9个采样时间点(4、8、12、18、24、36、48、72和96 h)。在每次更新染毒溶液之前测定溶液的pH值,每天更新相应pH值的染毒溶液。收集染毒初始时刻和染毒溶液更新之前的溶液各5 mL,每个浓度制备2个平行样待测浓度。
2.4 取样和理化分析
在每个采样时间点,记录幼鱼的死亡率,并收集染毒组和对照组(超纯水)中存活的幼鱼,每个浓度设置3个平行样,每个平行收集30条幼鱼至1.5 mL离心管,用超纯水洗净幼鱼,然后冷藏在-20 ℃下用于进一步分析。收集的染毒溶液经0.45 μm的膜(Whatman)过滤后待测。
实验后,将冷冻的幼鱼样品在电热恒温干燥箱(中环有限责任公司,天津,中国)在(60±0.5) ℃下干燥48 h至恒重,分别称重,并做记录,然后将1 mL浓HNO3(科密欧,优级纯,70%)加入1.5 mL离心管并在(80±2) ℃水浴消解(恒温水浴锅 HWS28,金坛,中国郑州),然后用一次性注射器(1 mL)带0.45 μm的滤头(Whatman)过滤。所有染毒溶液和幼鱼样品经过70%HNO3酸化,以达到1%的酸浓度后存储在4 ℃冰箱中待测。采用电感耦合等离子体-质谱联用仪(ICP-MS,ELAN DRC-E,珀金埃尔默,美国)对样品中金属的浓度进行测定。以不同时间点的初始和终点溶液中金属的平均浓度作为实际染毒浓度进行数据分析。
2.5 统计分析
染毒溶液中Cd或Pb的化学形态使用Visual MINTEQ(Visual MINTEQ Ver. 3.1,https://vminteq.lwr.kth.se/)计算。该模型的输入参数包括水温、溶液pH值、Cd2+或Pb2+、Cl-、和
的浓度。在所有的实验组中,在pH范围为4.5～6.5测试体系中Cd或Pb浓度的99%以上以游离金属离子Cd2+或Pb2+形态存在,因为溶液中只有Cd2+或Pb2+、Cl-、和
没有其他组分(如溶解性有机碳)存在。
H+与配体的络合常数(KHBL)是通过半数致死浓度(LC50Cd2+或LC50Pb2+)值与染毒溶液中H+的浓度(cH+)的线性回归的斜率和截距比值得到。使用建模软件R 3.1.2(http://www.R-project.ORG/)中“DeSolve”软件包估计参数,拟合幼鱼体内金属浓度实验数据得到TK参数(以Cd为例,JCd,max、KCdBL和kCd,out值)。拟合幼鱼死亡率和体内金属浓度之间关系的实验数据得到TD参数threshold和kk值。
使用建模软件R 3.1.2,用基于氢离子与配体络合常数的TK-TD模型分别拟合不同pH(4.5、5.5和6.5)的Cd和Pb的染毒溶液中,随着时间增加的金属在斑马鱼幼鱼体内的积累和产生的毒性。
3 结果(Results)
3.1 TK-TD模型参数求解
3.1.1 H+与配体络合常数KHBL求解
Cd染毒斑马鱼幼鱼24 h的LC50Cd2+与cH+呈显著的正相关关系(r2=0.83,P<0.001)(图2)。随着染毒溶液pH由5.5降到4.5,LC50Cd2+由4.59×10-6 mol·L-1升高至5.64×10-5 mol·L-1。因此,H+对Cd毒性的抑制效应应当在基于KHBL的TK模型(式(5))中考虑。KHBL是通过LC50Cd2+值与cH+的线性回归方程的斜率和截距比值得到关于Cd的KHBL,logKHBL=5.25(图2;式(9))。同样地,Pb暴露斑马鱼幼鱼24 h的LC50Pb2+与cH+呈显著的正相关关系(r2=0.92,P<0.001)(图2)。由LC50Pb2+值与染毒溶液中cH+的线性回归方程得到关于Pb的KHBL,logKHBL = 5.23(图2;式(10))。
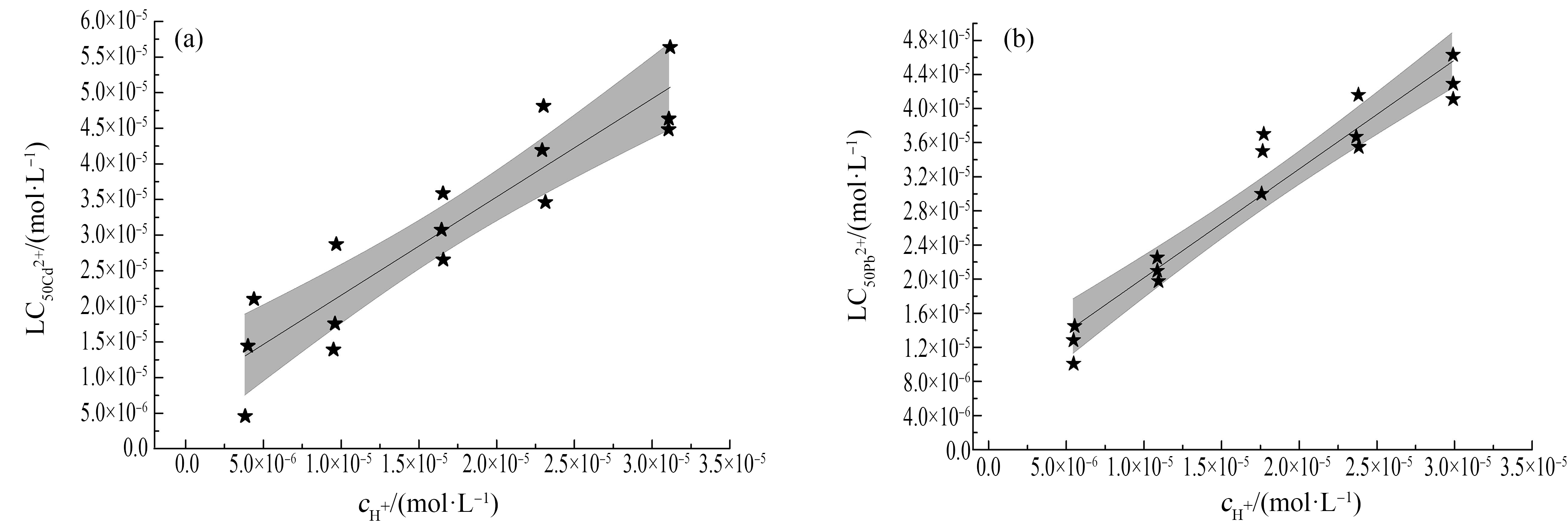
图2 Cd(a)和Pb(b)单独染毒幼鱼24 h后,溶液中Cd和Pb的半数致死浓度(LC50Cd2+和LC50Pb2+)和cH+的线性关系
注:实线代表线性拟合曲线,灰色线代表拟合曲线的95%置信区间。
Fig. 2 Median lethal concentrations of metal toxicity (LC50Cd2+ and LC50Pb2+) for zebrash larvae as a function of cH+after single exposure to Cd or Pb
Note: The solid lines represent the linear regression lines and the grey lines represent the 95% con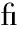dence interval.
LC50Cd2+ = 1.38×cH+ + 7.77×10-6(r2 = 0.83,P<0.001)
(9)
LC50Pb2+= 1.27×cH+ + 7.38×10-6(r2 = 0.92,P<0.001)
(10)
3.1.2 TK参数和TD参数求解
如图3所示,拟合幼鱼体内Cd或Pb浓度实验数据得到TK参数JM,max、KMBL和kM,out值。拟合幼鱼死亡率和体内Cd或Pb浓度之间关系的实验数据得到TD参数threshold和kk值。表1中列出TK-TD模型中所有参数值,即,KHBL、Cd或Pb的JM,max、KMBL、kM,out、threshold、kk和斑马鱼幼鱼初始质量(α)。在短时间的染毒实验中,幼鱼生长速率(β)可忽略不计,并假定为零。CM,int和hb的初始值设定为零。
表1 关于Cd和Pb的TK-TD模型参数
Table 1 Parameter values of TK-TD models of Cd and Pb
参数Parameter单位UnitCdPbTKJM,maxμg·g-1·h-111.78±0.43119.35±4.51KMBLL·mol-1(4.73±0.32)×105(8.27±0.28)×104KHBLL·mol-1(1.77±0.21)×105(1.72±0.15)×105kM,outh-10.0539±0.00210.0455±0.0015cM2+mol·L-18.89×10-74.83×10-6cH+mol·L-11.00×10-71.00×10-7αg0.00150.0015TDthreshold μg·g-111.39±1.24301.46±5.89kkg·μg-1·h-1(1.49±0.27)×10-3(3.47±0.54)×10-4
注:各参数的意义,见图1和正文中式(1)～(8)的说明。
Note: For the meaning of individual parameters, see Fig.1 and the explanation for Eqs. (1)～(8) in the text.
图3 0～96 h 0.1 mg·L-1 Cd (a) (b)和1 mg·L-1 Pb (c) (d)染毒幼鱼后金属在幼鱼体内的积累量和幼鱼存活率
注:实线表示金属在体内的积累量和幼鱼存活率模型拟合值。
Fig. 3 Comparison between observed and modeled internal concentration (accumulation) and survival fraction in zebrafish larvae of 0.1 mg·L-1 of Cd (a) (b) and 1 mg·L-1 of Pb (c) (d) during the 96 h exposure
Note: The solid lines are modeled values of internal concentration (accumulation) and survival fraction.
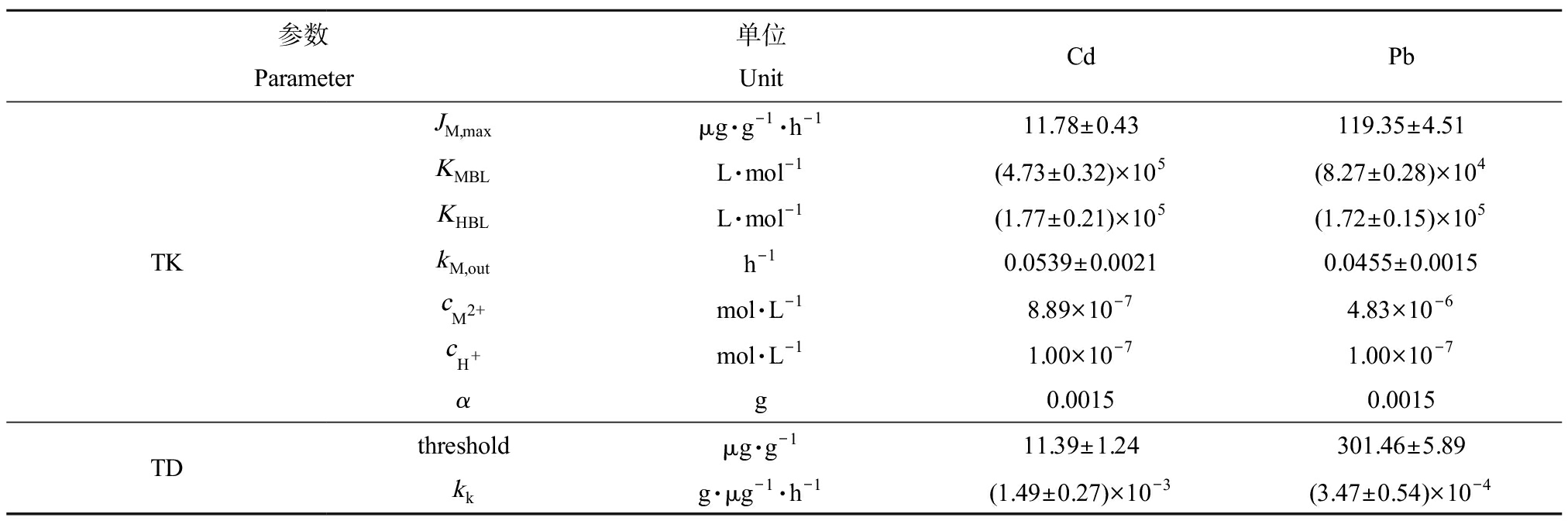
精确估计结合于不同水生生物BL上金属的浓度,需要了解金属或水生生物之间的差异。在本研究中,Cd2+和Pb2+与斑马鱼幼鱼BL络合常数(KCdBL和KPbBL)在大型溞(Daphnia magna)体内的络合常数值的范围内(2.38～7.96)(表2)[18]。logKHBL值低于大型溞(Daphnia magna)和网纹溞(Ceriodaphnia dubia)中得到的值[19-20],但高于裸腹溞(Moina dubia)中得到的值[21]。此外,Pb的最大吸收速率(Jmax)比Cd大约3倍(表1)。金属对生物毒性的增加是由于金属具有较低的threshold或较高的kk,或两者都有。Cd的kk是Pb的4倍。Cd和Pb的threshold相差30倍(表1)。通过金属的threshold可以倒推水溶液中金属的无效应浓度。然而,该值不能直接外推到其他水化学条件的环境中,因为在不同水化学条件下金属的生物有效浓度显著不同[22]。
表2 H+、Cd2+和Pb2+与不同生物的配体络合常数比较
Table 2 Comparison of binding constants of H+, Cd2+, and Pb2+ with ligands of different organisms
水生生物Aquatic organism络合常数(log)Binding constant (log)KHBLKCdBLKPbBL文献来源References网纹溞 Ceriodaphnia dubia7.60NANA[19]大型溞 Daphnia magna5.40NANA[19-20]大型溞 Daphnia magna8.797.96NA[10]网纹溞 Ceriodaphnia dubia4.70NANA[23] 裸腹溞 Moina dubia3.03NA2.38[24]斑马鱼幼鱼 Danio rerio larvae5.25±0.055.67±0.034.91±0.05本研究 This study
注:NA表示未分析。
Note: NA is not analyzed.
3.2 TK-TD模型验证
3.2.1 TK模型预测金属在幼鱼体内的积累
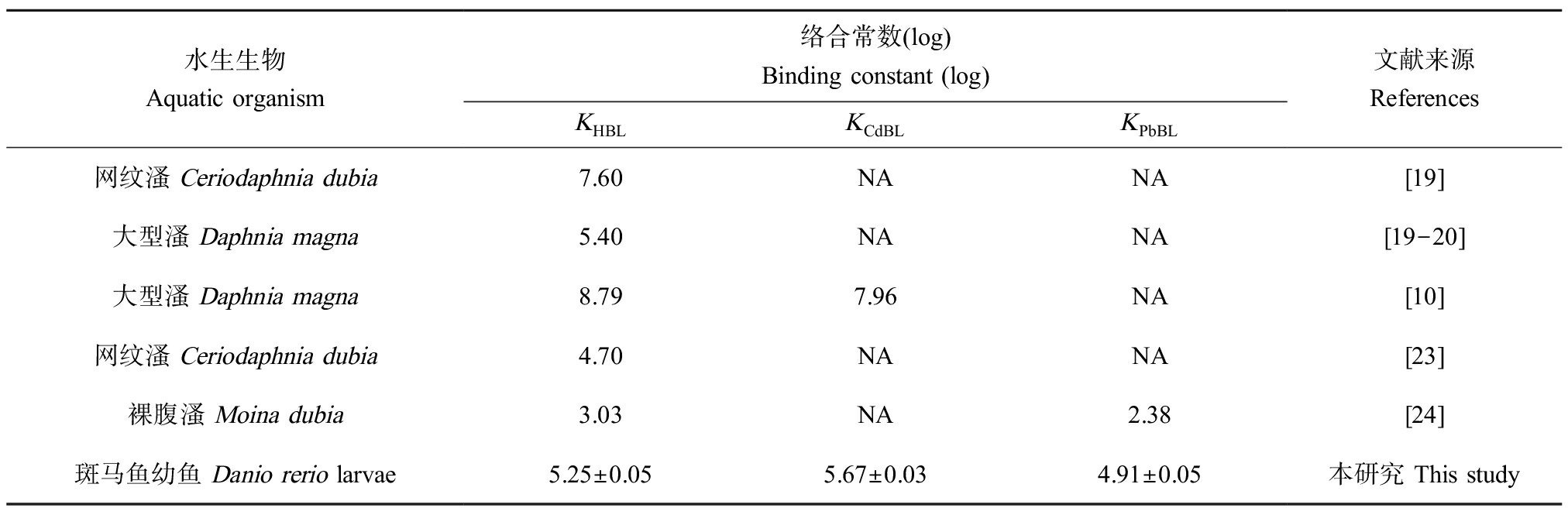
不同的pH值(4.5、5.5和6.5)的0.1 mg·L-1 Cd或1 mg·L-1 Pb溶液暴露下,Cd或Pb在幼鱼体内的积累量随着时间的增加而增加(图4)。各金属在幼鱼体内的积累量是关于染毒溶液中H+的浓度和染毒时间的函数。在染毒开始的8 h内,溶液中H+的浓度没有对金属在幼鱼体内的积累产生显著影响,但>8～72 h之间某一染毒时间时,体内Cd或Pb浓度随着H+浓度增加而显著降低(P<0.001)。以幼鱼暴露于pH为6.5的Cd或Pb溶液为例,在72 h时,Cd和Pb在幼鱼体内的最高浓度分别为(60.7±0.35) μg·g-1和(722±14.0) μg·g-1。在所有实验组中,体内金属浓度随着染毒时间的增加而增加并在约72 h后趋于平衡。TK模型式(4)能合理地预测体内金属浓度随着时间的变化并在统计学上具有显著意义(P<0.001)。Cd和Pb积累的实验观测值和模型预测值的1∶1依赖系数(r2)和均方根误差(RMSE)分别是0.89、3.76和0.83、34.2。
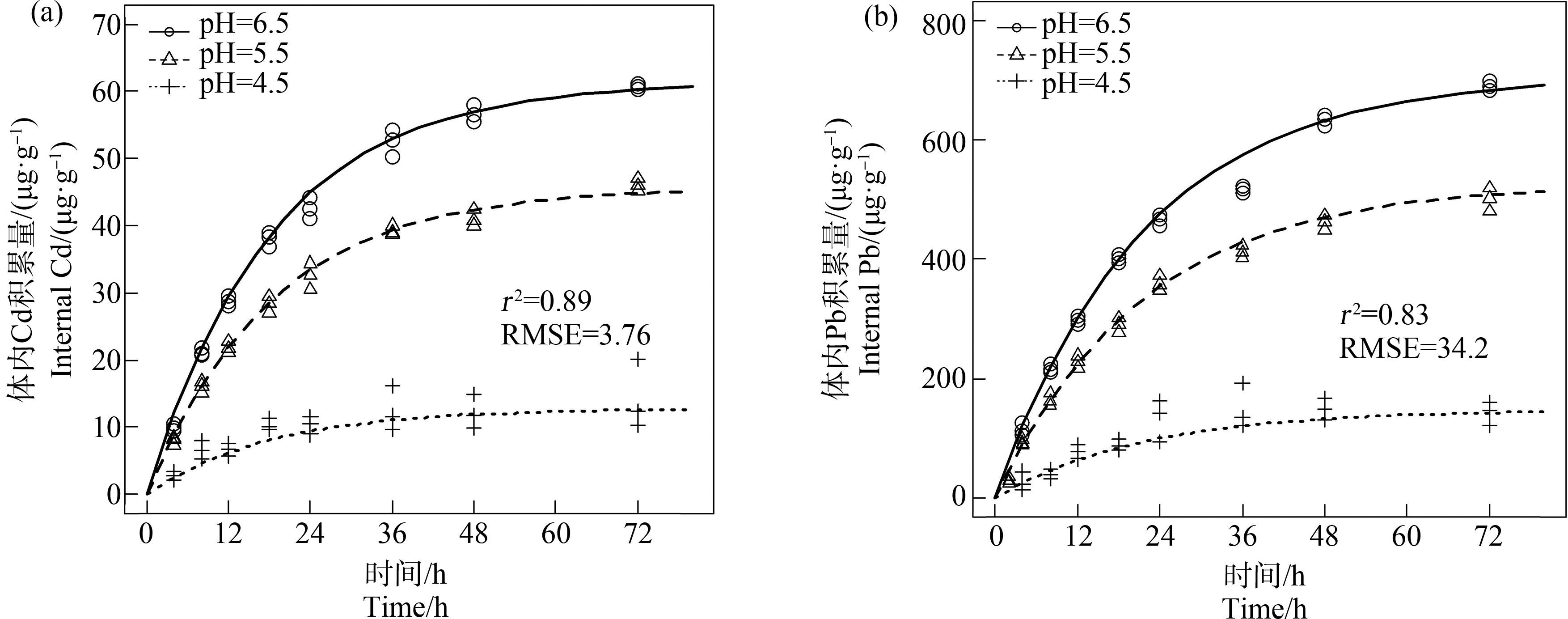
图4 0～96 h幼鱼在不同pH染毒溶液中金属0.1 mg·L-1 Cd (a)、1 mg·L-1 Pb (b)在幼鱼体内的积累量模型预测值和观测值的比较
注:加号、三角形、圆形表示溶液在pH 4.5、5.5和6.5下金属在体内的积累量实验观测值,点线、虚线和实线分别表示溶液在pH 4.5、5.5和6.5下金属在体内的积累量模型预测值;其中,在96 h时,幼鱼全部死亡,所以没有分析体内金属累积量;r2是观测值和预测值1∶1线的依赖系数,RMSE是观测值和预测值的均方根误差。
Fig. 4 Comparison between observed and modeled internal concentration (accumulation) in zebra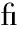sh larvae of 0.1 mg·L-1 of Cd (a) and 1 mg·L-1 of Pb (b) during the 96 h exposure in different pH of solutions
Note: Plus, triangles and circles are observed values, and dotted lines, dashed lines, and solid lines are modeled values at pH 4.5, 5.5 and 6.5, respectively; observed internal concentrations for 96 h were not analyzed because no surviving animals were collected; r2 is the coefcient of dependence of the 1∶1 line; RMSE is root mean square error.
3.2.2 TD模型预测金属的毒性
不同的pH值(5.5、6.5和7.0)的0.1 mg·L-1 Cd或1 mg·L-1 Pb溶液暴露下,幼鱼的存活率随着染毒时间的增加而降低(图5)。Cd或Pb对幼鱼的毒性是关于染毒溶液中H+的浓度和染毒时间的函数。在某一暴露时间点,幼鱼的存活率随着溶液中H+浓度的增加而增加。在Cd染毒实验开始4 h内和Pb染毒实验开始12 h内,溶液中H+的浓度对金属毒性的缓解作用不明显。Cd染毒幼鱼8 h后和Pb染毒幼鱼18 h后,幼鱼死亡率迅速增加。暴露于不同pH值条件下的Cd或Pb溶液96 h后,各染毒组中幼鱼全部死亡。TD模型式(5)～(7)能合理地预测幼鱼存活率(P<0.001),模型预测值与实验观测值十分吻合。Cd和Pb的毒性的模型预测值和实验观测值的1∶1依赖系数(r2)和均方根误差(RMSE)分别是0.92、0.024和0.90、0.038。
图5 0～96 h幼鱼在不同pH染毒溶液0.1 mg·L-1 Cd (a)和1 mg·L-1 Pb (b)中存活率模型预测值和观测值的比较
注:加号、三角形、圆形表示溶液在pH 4.5、5.5和6.5下幼鱼存活率实验观测值,点线、虚线和实线分别表示溶液在pH 4.5、5.5和6.5下幼鱼存活率模型预测值;TD模型的参数估计如表1所示,r2是观测值和预测值1∶1线的依赖系数,RMSE是观测值和预测值的均方根误差。
Fig. 5 Comparison between observed and modeled survival fraction of zebrash larvae during the 96 h exposure to 0.1 mg·L-1 of Cd (a) and 1 mg·L-1 of Pb (b) in different pH of solutions
Note: Plus, triangles and circles are observed values, and dotted lines, dashed lines, and solid lines are modeled values at pH 4.5, 5.5 and 6.5, respectively; the estimated toxicodynamic parameters are listed in Table 1; r2 is the coefficient of dependence of the 1∶1 line; RMSE is root mean square error.
4 讨论(Discussion)
4.1 H+对Cd或Pb毒性的影响
H+对Cd或Pb毒性显著的抑制作用表明,H+、Cd2+和Pb2+可能通过相同的传输路径进入体内,并且H+通过与Cd2+或Pb2+竞争结合位点而减少幼鱼对Cd或Pb的积累,从而起到了保护作用。这一研究结果支持了BLM的一个重要假设,即H+与Cd2+或Pb2+竞争同一传输位点[25-26]。同样地,染毒溶液pH在5.0到7.0范围内随着H+浓度的增加显著地抑制Cd2+对大型溞(Daphnia magna)的毒性[10]。Cd或Pb染毒实验表明,H+与生物配体的结合影响了有毒离子的积累从而影响了金属的毒性。因此,本研究开发了一个考虑溶液中H+竞争作用对Cd或Pb在幼鱼体内积累影响的Cd-或Pb-TK模型。
4.2 积累
>8～72 h这个时间段是急性毒性实验中真正起毒性作用的阶段,溶液中H+的浓度对金属在幼鱼体内积累的影响越来越明显。在染毒开始时,体内金属的浓度取决于染毒时间和溶液中H+的浓度。体内Cd或Pb浓度随着染毒时间的增加而增加,大约72 h后达到平衡。达到平衡后,体内浓度仅和溶液中H+浓度有关。溶液中H+浓度增加,Cd和Pb在幼鱼体内的积累量会显著下降,这表明H+抑制Cd和Pb在斑马鱼体内的积累。这可能由于H+和金属离子共用同一生物转运途径,结合到BL上的金属的量随着溶液中H+的增加而显著下降。也就是说,可通过增加溶液中H+的浓度来减少幼鱼对Cd和Pb的积累。此外,每个暴露时间点,低pH值(4.5)的染毒溶液比高pH值(6.5)的染毒溶液中H+抑制Cd或Pb的生物吸收明显,因为Cd或Pb的积累与溶液中H+浓度呈显著负相关关系。
4.3 毒性
当金属在幼鱼体内的浓度超过了一定的安全阈值时,会导致幼鱼死亡率明显增加[27]。以往研究中TD模型建立在临界体内残留(CBR)方法的基础上[28],并且假设生物个体具有不同的毒性敏感性和当体内金属浓度达到一定值时会发生死亡,死亡率可以用剂量效应方程来解释[28]。在一定浓度长期暴露情况下,CBR模型预测一定数量的受试生物可以长久地存活(不包括背景死亡率)[28]。相反地,本研究中的TD模型预测死亡率证明,当染毒时间足够长,任何导致受试生物发生部分死亡的暴露浓度最终会消灭所有受试生物。
溶液中H+的浓度对金属毒性作用的影响随着时间的增加而变得尤为明显(Cd:>8～96 h,Pb:>12～96 h)。以幼鱼暴露于pH为6.5的Cd或Pb溶液为例,Cd染毒8 h和Pb染毒12 h后,幼鱼死亡率迅速增加。在8 h时,Cd在幼鱼体内的累积量为(21.1±0.53) μg·g-1,超过了Cd的毒性安全阈值(11.39±1.24) μg·g-1。在12 h时,Pb在幼鱼体内的累积量为(298±7.01) μg·g-1,未超过Pb的毒性安全阈值(301.46±5.89) μg·g-1。这一结果表明,在96 h染毒期内,Pb的急性毒性小于Cd的急性毒性。
TD模型通过因果关系链将Cd或Pb暴露浓度、体内积累量与毒性效应联系起来。在本研究中,CCd,int或CPb,int表示体内Cd或Pb的浓度,取代了以往研究中用染毒溶液中金属的浓度与毒性效应建立的联系。然而,体内Cd或Pb的浓度不等于体内Cd或Pb毒性作用剂量。体内Cd或Pb毒性作用剂量与体内Cd或Pb浓度呈正相关关系[27]。因此,TD过程是由超过安全阈值(threshold)的那部分Cd或Pb的量来决定(即毒性作用剂量,式(6)),这部分Cd或Pb可与靶位点(靶器官)互相作用[27]。TD模型中参数threshold和kk符合现有知识对金属毒性作用的研究。因此,TD模型对Cd或Pb毒性的预测大概率可推广至不同的水化学条件。
4.4 模型适用性分析
与传统剂量效应模型相比,本研究中TK-TD模型更具有生物学相关性,并引入了金属与物种结合特征参数(即金属与生物配体络合常数(KCdBL和KPbBL))和水化学条件(例如H+)对金属毒性的影响。水溶液中金属的吸收速率在很大程度上取决于溶液水化学条件。因此,在一种金属溶液里计算得到的生物体内积累量CM,int不能直接外推至另一种溶液中。例如,在pH值4.5到6.5的染毒溶液体系中,由于HCl的加入,Cl-量随着H+的加入而发生约0.32～31.6 μmol·L-1的变化。本研究中H+和Cl-额外的加入量对对照组中幼鱼发育没有明显影响,并且没有对实验结果产生任何显著影响。此外,当染毒溶液pH值低于4.0,高浓度H+会导致幼鱼死亡。本研究考虑H+对金属生物体内积累量和毒性的影响过程,为今后研究其他阳离子对金属生物体内积累量和毒性的影响过程提供技术框架。此外,H+和金属离子竞争生物配体的作用机制为2种金属竞争生物吸收位点提供新思路。
本研究中TK-TD模型的框架在理论上稍加修改可适用于其他水生生物,以往研究中关注金属某一暴露时间点的毒性(如死亡率),缺乏时间过程的实验数据(金属生物体内积累量及对应的死亡率),无法进一步验证模型适用性和范围。总体来说,这些模型都是灵活的,可以很容易地适用于对金属的生物蓄积性和毒性的机制的更深入认识。
4.5 环境意义
定量预测重金属在水环境中的毒性效应可以提高重金属水生态风险评估准确率。在本研究中,建立了基于KHBL的TK-TD模型,明确地将随着时间变化的金属在体内的积累与个体水平上的毒性效应(死亡率)之间建立量效关系。该模型以基于物种特征的BL(生物膜受体)的参数KMBL、KHBL和染毒条件(例如,溶液的pH值、金属的浓度和染毒时间)作为模型的变量,用于预测随着时间的变化在水环境不同pH条件下生物体内金属积累和产生的急性毒性。未来的研究试图将其他阳离子和配体络合常数整合到TK-TD模型中,提高和改善该模型在自然水体中预测金属毒性的潜力。
[1] Zhang Y L, Zhang L J, Liang X J, et al. Competitive exchange between divalent metal ions [Cu(Ⅱ), Zn(Ⅱ), Ca(Ⅱ)] and Hg(Ⅱ) bound to thiols and natural organic matter [J]. Journal of Hazardous Materials, 2022, 424(Pt A): 127388
[2] McDonald S, Holland A, Simpson S L, et al. Metal forms and dynamics in urban stormwater runoff: New insights from diffusive gradients in thin-films (DGT) measurements [J]. Water Research, 2021, 209: 117967
[3] Wetzel O, Hosseini S, Loza K, et al. Metal-ligand interface and internal structure of ultrasmall silver nanoparticles (2 nm) [J]. The Journal of Physical Chemistry B, 2021, 125(21): 5645-5659
[4] DeForest D K, Gensemer R W, van Genderen E J, et al. Protectiveness of water quality criteria for copper in western United States waters relative to predicted olfactory responses in juvenile Pacific salmon [J]. Integrated Environmental Assessment and Management, 2011, 7(3): 336-347
[5] Liu X Y, Tu M C, Wang S P, et al. Research on freshwater water quality criteria, sediment quality criteria and ecological risk assessment of triclosan in China [J]. The Science of the Total Environment, 2022, 816: 151616
[6] DeForest D K, Ryan A C, Tear L M, et al. Comparison of multiple linear regression and biotic ligand models for predicting acute and chronic zinc toxicity to freshwater organisms [J]. Environmental Toxicology and Chemistry, 2023, 42(2): 393-413
[7] Gao Y F, Zhu J X, He A. Effect of dissolved organic matter on the bioavailability and toxicity of cadmium in zebrafish larvae: Determination based on toxicokinetic-toxicodynamic processes [J]. Water Research, 2022, 226: 119272
[8] Chung J, Lee J H, Hwang D S, et al. Comparison of the estimation methods from acute to chronic biotic ligand model-based predicted no-effect concentrations for nickel in freshwater species [J]. Environmental Toxicology and Chemistry, 2023, 42(4): 914-927
[9] Croteau K, Ryan A C, Santore R, et al. Comparison of multiple linear regression and biotic ligand models to predict the toxicity of nickel to aquatic freshwater organisms [J]. Environmental Toxicology and Chemistry, 2021, 40(8): 2189-2205
[10] Liang W Q, Xie M W, Tan Q G. Making the biotic ligand model kinetic, easier to develop, and more flexible for deriving water quality criteria [J]. Water Research, 2021, 188: 116548
[11] Liu Y H, Yao L, Huang Z, et al. Enhanced prediction of internal concentrations of phenolic endocrine disrupting chemicals and their metabolites in fish by a physiologically based toxicokinetic incorporating metabolism (PBTK-MT) model [J]. Environmental Pollution, 2022, 314: 120290
[12] Nys C, Vlaeminck K, van Sprang P, et al. A generalized bioavailability model (gBAM) for predicting chronic copper toxicity to freshwater fish [J]. Environmental Toxicology and Chemistry, 2020, 39(12): 2424-2436
[13] Hommen U, Schmitt W, Heine S, et al. How TK-TD and population models for aquatic macrophytes could support the risk assessment for plant protection products [J]. Integrated Environmental Assessment and Management, 2016, 12(1): 82-95
[14] Gao Y F, Kang L L, Zhang Y, et al. Toxicokinetic and toxicodynamic (TK-TD) modeling to study oxidative stress-dependent toxicity of heavy metals in zebrafish [J]. Chemosphere, 2019, 220: 774-782
[15] Armitage J M, Hughes L, Sangion A, et al. Development and intercomparison of single and multicompartment physiologically-based toxicokinetic models: Implications for model selection and tiered modeling frameworks [J]. Environment International, 2021, 154: 106557
[16] Kajiura M. Stochastic estimation of the distribution of soil water repellency on the soil surface in a humid-temperate forest [J]. Hydrological Processes, 2022, 36(5): e14576
[17] Akimenko M A, Johnson S L, Westerfield M, et al. Differential induction of four msx homeobox genes during fin development and regeneration in zebrafish [J]. Development, 1995, 121(2): 347-357
[18] Jho E H, An J, Nam K. Extended biotic ligand model for prediction of mixture toxicity of Cd and Pb using single metal toxicity data [J]. Environmental Toxicology and Chemistry, 2011, 30(7): 1697-1703
[19] Nys C, Janssen C R, Mager E M, et al. Development and validation of a biotic ligand model for predicting chronic toxicity of lead to Ceriodaphnia dubia [J]. Environmental Toxicology and Chemistry, 2014, 33(2): 394-403
[20] Nys C, Janssen C R, De Schamphelaere K A C. Development and validation of a chronic Pb bioavailability model for the freshwater rotifer Brachionus calyciflorus [J]. Environmental Toxicology and Chemistry, 2016, 35(12): 2977-2986
[21] Wang X D, Hua L, Ma Y B. A biotic ligand model predicting acute copper toxicity for barley (Hordeum vulgare): Influence of calcium, magnesium, sodium, potassium and pH [J]. Chemosphere, 2012, 89(1): 89-95
[22] Bawa-Allah K A, Bulama H, Hamzat S A, et al. Predicting metal bioavailability and risk of toxicity in Nigerian surface waters: Are the existing user-friendly bioavailability tools applicable? [J]. Environmental Toxicology and Chemistry, 2022, 41(10): 2537-2547
[23] Santore R C, Croteau K, Ryan A C, et al. A review of water quality factors that affect nickel bioavailability to aquatic organisms: Refinement of the biotic ligand model for nickel in acute and chronic exposures [J]. Environmental Toxicology and Chemistry, 2021, 40(8): 2121-2134
[24] Pham H T, Vu L D, Lê N C, et al. Application and validation of a biotic ligand model for calculating acute toxicity of lead to Moina dubia in lakes of Hanoi, Vietnam [J]. Environmental Science and Pollution Research International, 2022, 29(28): 42005-42015
[25] Clément B, Felix V, Bertrand V. The toxicity of cadmium-copper mixtures on daphnids and microalgae analyzed using the biotic ligand model [J]. Environmental Science and Pollution Research International, 2022, 29(20): 29285-29295
[26] Mit C, Bado-Nilles A, Daniele G, et al. The toxicokinetics of bisphenol A and its metabolites in fish elucidated by a PBTK model [J]. Aquatic Toxicology, 2022, 247: 106174
[27] Jager T, Albert C, Preuss T G, et al. General unified threshold model of survival—A toxicokinetic-toxicodynamic framework for ecotoxicology [J]. Environmental Science &Technology, 2011, 45(7): 2529-2540
[28] Wen Y, Su L M, Qin W C, et al. Investigation of critical body residues and modes of toxic action based on injection and aquatic exposure in fish [J]. Water, Air, &Soil Pollution, 2015, 226(6): 174
ned TK-TD model can accurately predict the accumulation and acute toxicity of Cd and Pb in zebra