-
膜生物反应器(membrane bioreactor, MBR)是将膜分离单元、生物处理单元相结合的一种新型水处理技术。因其具有占地面积小、安装灵活、污染物去除率高、出水质量好且运行效果稳定等特点,所以被广泛应用在污水处理中[1]。在MBR工艺中,膜分离单元主要采用平板膜和中空纤维膜2种形式,两者具有不同的特性[2]。为了结合2种形式的优点,新型MBR平板膜[3-7]的研制获得了国内外越来越多研究者的关注。其中,超薄平板膜的提出优化了常规平板膜的原有特性。如表1所示,超薄平板膜具有装填紧密、抗污染性好、运行维护简单等技术优势。然而,若使这种新型平板膜MBR在实际运行中得到高效稳定的应用,进而抑制膜污染问题,超薄平板膜MBR的曝气条件优化成为一个重要的研究方向。
计算流体动力学(computational fluid dynamics, CFD)是在经典流体动力学与数值计算方法的基础上,通过计算机数值计算和图像显示对相关物理现象所做的分析[8-9]。由于MBR中复杂多相流的流态特征与膜面剪切力分布密切相关[10],而且,在膜堆当中,仅通过实验难以对流体动力问题进行充分分析,故CFD已逐渐成为MBR中多相流准确模拟[11]的一种高精度、低成本的分析手段[12],其可以直观地表征MBR在不同曝气条件下的流态分布。然而,目前MBR曝气条件优化的研究重点是单一分析曝气量、曝气管布置形式等因素[13-15],主要是分析反应器纵向剖面流速分布,而对横向和纵向剖面流速分布的综合分析较少。此外,大多数研究未充分考虑不同曝气量下的膜流态分布的特性以及膜面颗粒沉积概率。
本研究采用CFD Fluent软件,以高精度的网格对气液两相流进行三维数值模拟[16],研究了超薄平板膜MBR在不同曝气条件下的膜污染行为机制,分析了在不同曝气量(10∶1、15∶1、20∶1)下,气泡对膜表面的冲刷能力以及膜片的抖动效果,量化膜片表面的气泡冲刷强度,确定了平板膜堆在曝气情况下的死区。最终,给出超薄平板膜MBR运行的最优曝气策略,以期在理论方面推动新型平板膜MBR的优化分析进程。
-
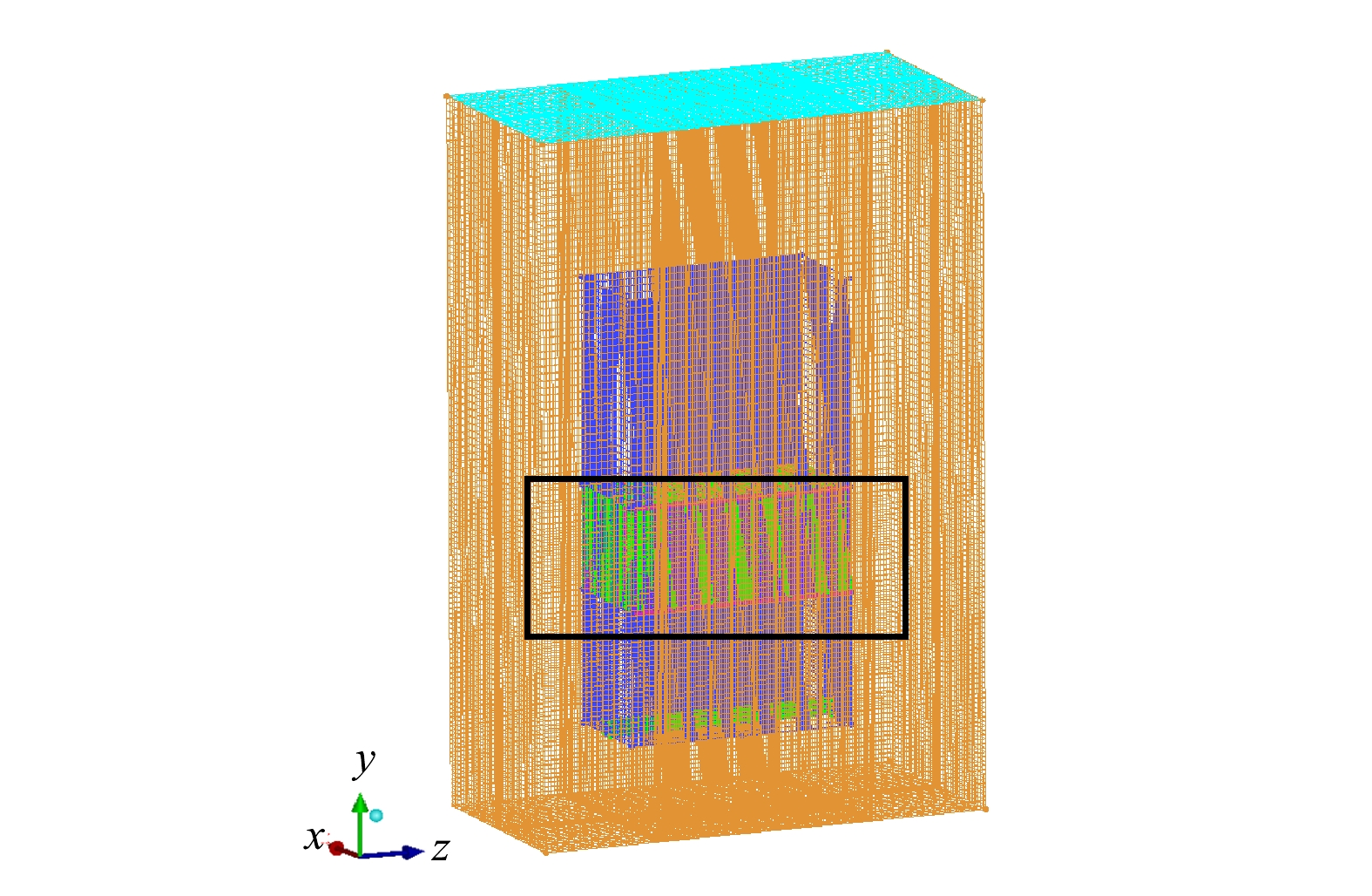
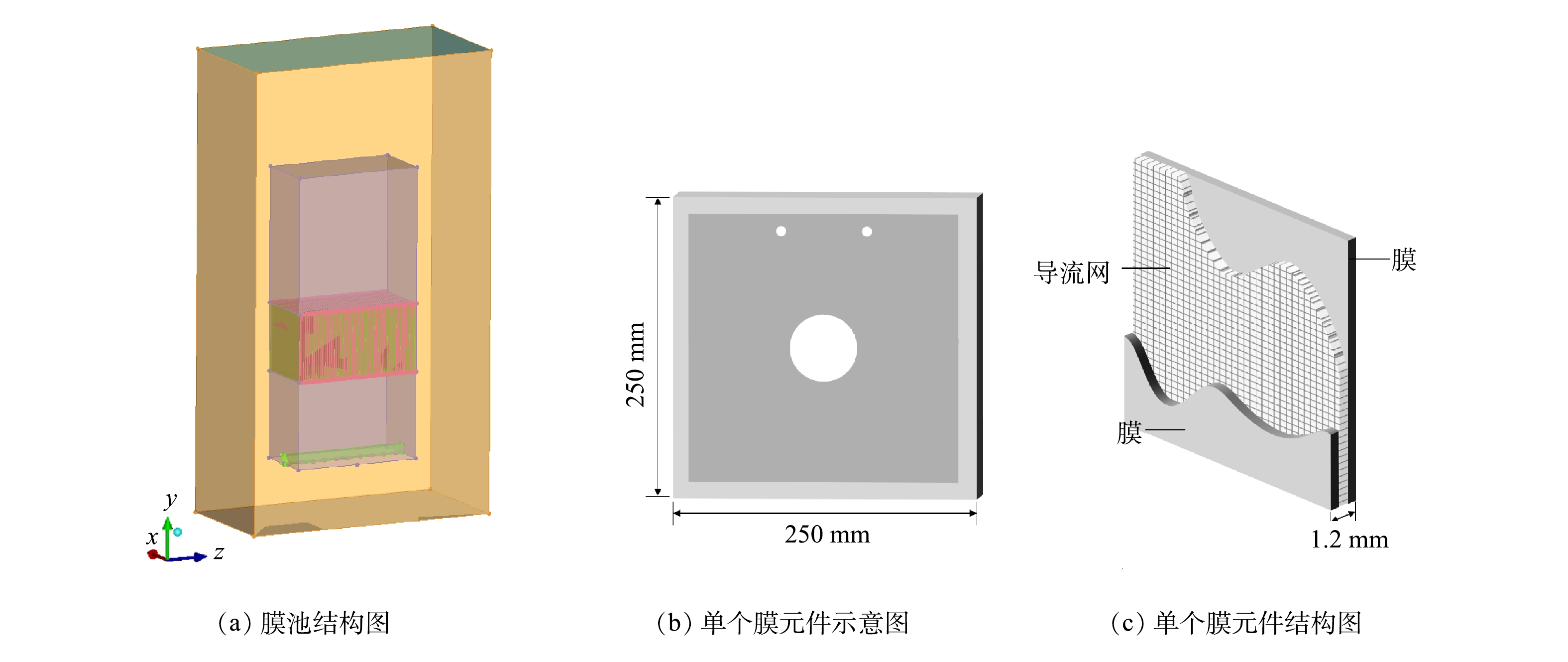
本研究选取超薄平板膜MBR作为研究对象。模拟对象结构如图1所示。其中,膜堆由64个膜元件组成,每个膜元件均由左右两层膜皮与中间的导流网构成,尺寸为250 mm×250 mm,7 mm的膜间距放置。按照MBR设计尺寸1∶1建立几何模型,反应器长500 mm,宽度250 mm,高度1 070 mm,以反应器宽度方向、高度方向、长度方向为x、y、z方向建立坐标系。在膜堆的正下方布设一只直径为32 mm,长度为500 mm的曝气管,且曝气管距离膜片底部320 mm,爆气孔直径5 mm,间距50 mm为计算水流在反应器内外的流动,设置反应器外围水域尺寸为1 000 mm×500 mm×1 700 mm。
-
CFD模拟的基本原理是通过数学方法将连续流体离散化,并在生成的网格上使用合适的算法求解一组控制方程。由于考虑到相间的交互作用,其控制方程主要包括守恒方程以及湍流和两相流方程。
首先,确定数学模型。在对反应器进行模拟时,除满足包括连续性方程、动量守恒方程、能量方程在内的基本守恒方程外,由于系统处于湍流状态的流动过程包含有不同组分的混合或相互作用,因此还要遵守组分守恒定律。连续性方程见式(1),动量守恒方程见式(2),能量守恒方程见式(3),组分守恒方程见式(4)。
式中:
$ \rho $ 为密度,kg·m−3;$ {u}_{i} $ 为第i相的平均速度矢量,m·s−1;t为时间,s;$ {u}_{j} $ 为第i相在t时刻点$ {x}_{j} $ 方向的速度分量;常数$ \mu $ 为粘度系数;p为压力;$ \rho {g}_{i} $ 为只考虑重力时,单位体积的第i相所受外力;T为温度;$ {c}_{\mathrm{p}} $ 为比热容;λ为热导率;$ {w}_{\mathrm{f}}{Q}_{\mathrm{f}} $ 为热能,kJ;$ {Y}_{\mathrm{f}} $ 为第i种组分的局部质量分数;D为扩散系数,m2·s−1;$ {w}_{\mathrm{f}} $ 为组分的质量分数。其次,明确物理模型及边界条件。本研究利用CFD Fluent软件对MBR中简化后的气液混合流[17]进行数值模拟。基于包括虚拟质量力(虚拟质量力系数为0.5)、曳力(universal-drag模型)、升力(Tomiyama模型)、湍流扩散(burns-et-al模型)、湍流交互(Sato模型)在内的气液相间作用力,考虑到反应器中液相的平均流动存在旋转、旋流流动及流线弯曲程度较大的情况,选择RNG k-ε湍流模型以更好地应对高应变率。由于气液两相作用力明显,故选取Eulerian多相流模型进行高精度计算,将水设为基本相,空气为第二相。
将MBR底部曝气管喷口设为速度入口,初始气泡直径为5 mm,顶部采用脱气式出口,且在运行过程中允许气体逸出不许液体流出;考虑到膜渗透速度远小于反应器内的特征速度,故膜面按照不可渗透壁面处理;根据收敛条件的判别依据[18],采用软件监测反应器截面的平均流速及进出口质量流量差的方法,得到收敛结果。
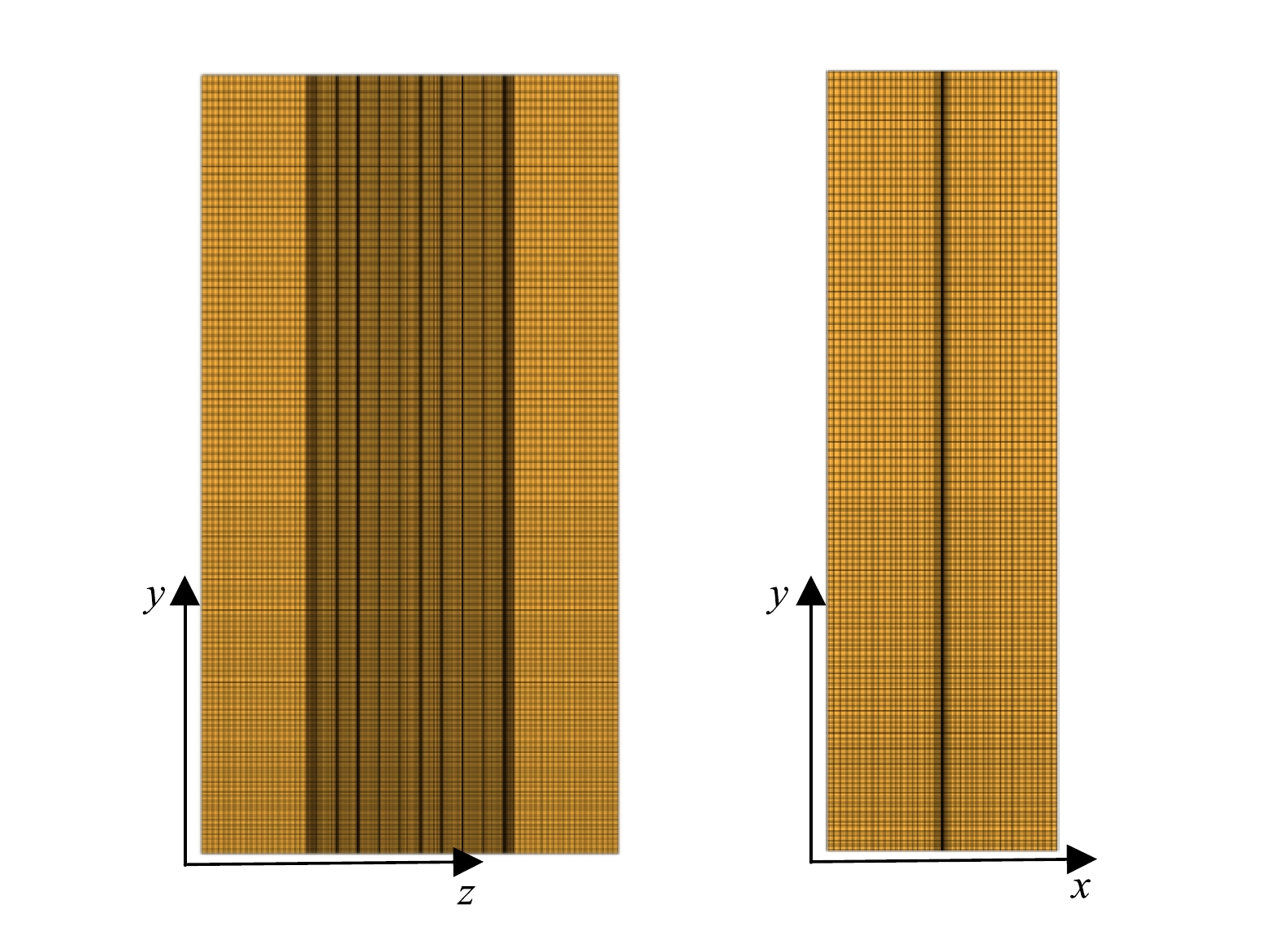
最后,确定计算域并进行网格划分。本研究中,由于采用的Eulerian模型考虑了多项相间作用力,对网格质量要求极高,因此,将曝气管简化为矩形曝气管,以减少网格畸变度。如图2所示,全部采用高质量六面体对计算域网格进行划分,得到的计算域网格为88×104个。这种划分方法可以大幅度减少网格总数,进而缩短非稳态过程的计算时间,有利于提高计算的精度并加快收敛速度。在此基础上,为获得更加精准的计算结果,对MBR反应器及曝气管区域进行网格加密(图3)。在图4中选取图2中的膜片区域网格进行划分,膜片之间的间距仅7 mm,同样采用六面体网格划分方式。
-
1)流场分析。主要对反应器横、纵剖面的流速分布、膜间流速分布进行流态模拟分析,针对不同分析角度截取不同位置的截面。通过模拟计算得到收敛后不同气水比条件下的结果图后,对比反应器中不同曝气量下的膜面冲刷情况及低速区占比特征。
2)膜污染分析。从宏观、微观相结合的角度[16]对膜面剪切力分布及膜面颗粒沉积概率进行了膜污染分析。在微观角度,分析微米级颗粒的受力,渗透流的阻力使颗粒倾向于向膜表面迁移,而式(5)表明颗粒迁离膜面的作用力主要包括影响小胶体颗粒的布朗扩散力、影响大直径颗粒的剪切诱导扩散力[19]和惯性升力[20]。当颗粒所受迁移至膜面的作用力与迁离膜面的作用力相等时,刚好不发生膜面沉积,称为临界状态[21],则此时颗粒的迁移通量即为通量的临界值。
式中:Jc为通量的临界值,L·(m2·h)−1;
$ {J}_{\mathrm{t}\mathrm{o}\mathrm{t}} $ 为临界状态下的颗粒迁移通量,L·(m2·h)−1;$ {J}_{\mathrm{B}} $ 为布朗扩散通量,L·(m2·h)−1;$ {J}_{\mathrm{S}} $ 为剪切诱导扩散通量,L·(m2·h)−1;$ {J}_{\mathrm{I}} $ 为侧向惯性升力作用通量,L·(m2·h)−1;在颗粒扩散沉积过程中,颗粒粒径小于1 μm的亚微米级颗粒的迁移机理以布朗扩散力为主,其临界状态下的扩散通量根据式(6)计算。但布朗扩散模型低估了颗粒在大颗粒和高剪切率条件下的回输能力,因而引出临界状态下的剪切诱导扩散通量[22]见式(7)。由于Davis和Sherwood提出的剪切诱导扩散力仍低估了浓度极化边界层中的扩散,惯性升力机制[23]被提出,在此力作用下通量按式(8)计算。
式中:
$ {\gamma }_{\mathrm{w}} $ 为剪切速率,$ {s}^{-1} $ ;$ \kappa $ 为玻尔兹曼常数,1.38×10−23 kg·m2·s−2;T为绝对温度,K;$ {\eta }_{\mathrm{f}} $ 为粘度,Pa · s;$ \alpha $ 为颗粒直径,m;L为膜长度,m;$ {\rho }_{\mathrm{f}} $ 为密度,kg·m−3;$ {\varphi }_{\mathrm{w}} $ 为颗粒在滤饼层边缘的体积分数,$ {\varphi }_{\mathrm{b}} $ 为颗粒在悬浮液中的体积分数,两者比值为浓差极化因子。综上所述,本研究中实验规模的MBR,可采用E值(式(9))表示膜面颗粒沉积概率[24]。
依据实际膜通量 J与临界通量Jc的大小关系进行判断:若J < Jc时,颗粒沉积概率较小;反之,颗粒在渗透拖曳力的作用下易于沉积。由式(9)可知,E =0.5为临界值,当E < 0.5时,E值越小,膜面受污染可能性越小。
-
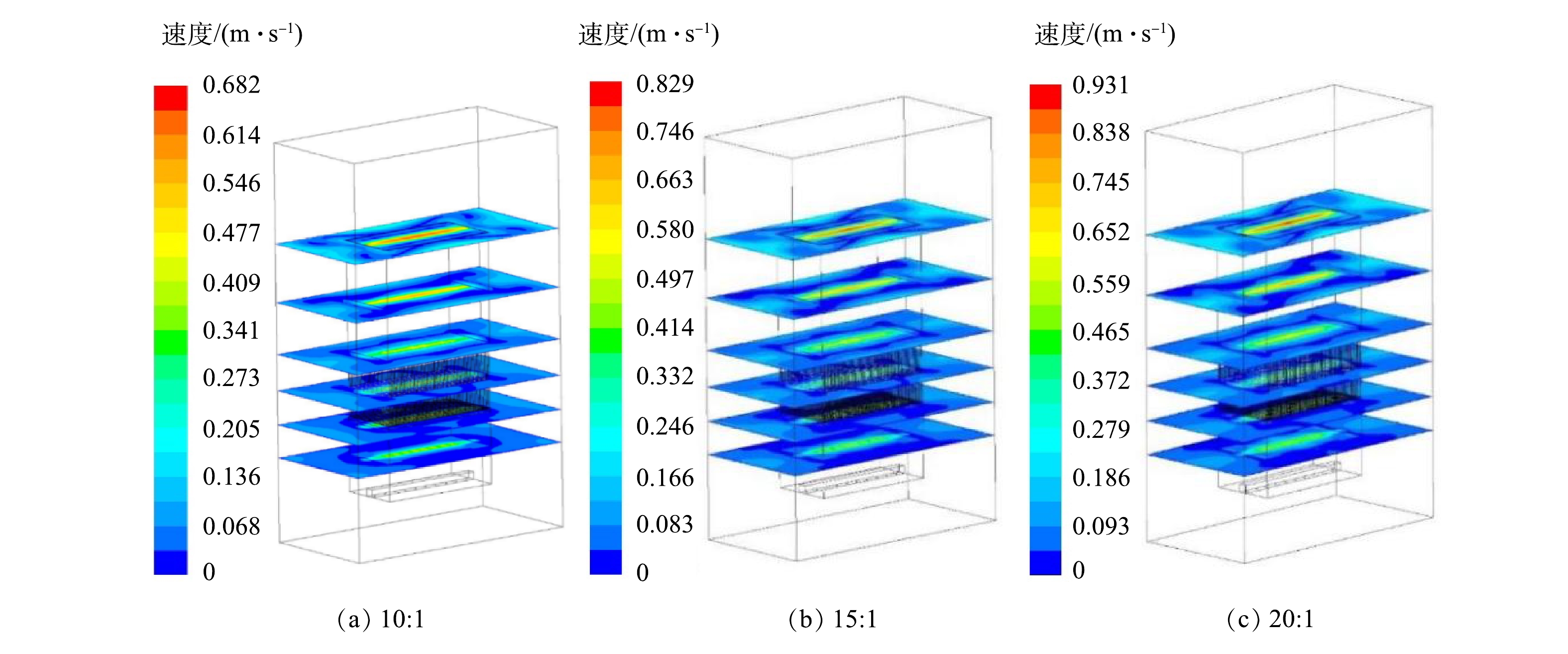
如图5所示,在3种曝气工况下,对截取的反应器中不同高度横截面的流速分布进行模拟,图中由蓝到红表示速度绝对值逐渐增大。同一高度下,位于中心位置的水流流速大,对膜片的冲刷效果明显,而四周流速较小。在膜堆区域,截面速度不为零,则水流与气流的结合引起膜面明显振动,将气泡推离膜面。随高度的增加,反应器横截面内速度分布的充满度有所改善,且整体横截面流速明显增加。这是由于水流在流动过程中随气泡的上升而加速,但仍存在流速分布不均匀性。针对不同高度,对比各气水比条件下的流速分布,可以看出改变气水比对横截面内流速分布影响较小。
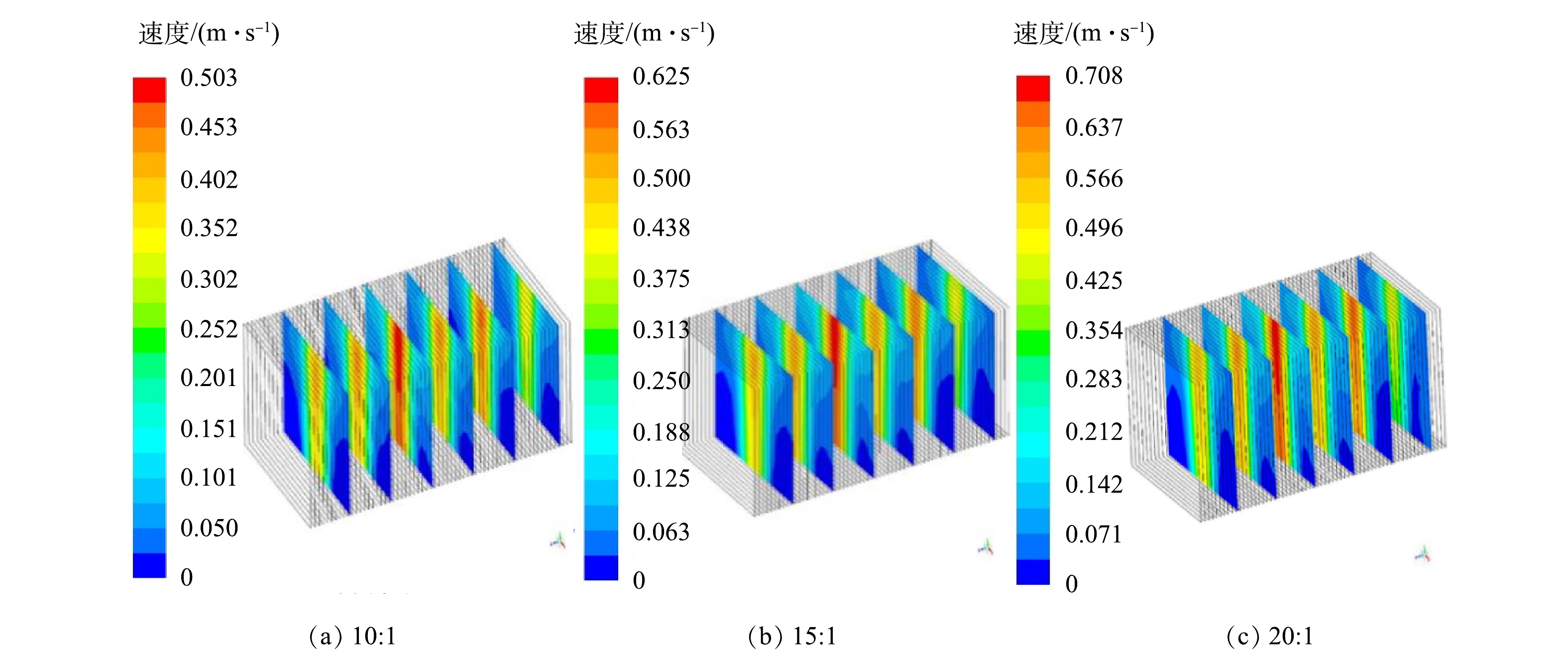
为了综合考虑横纵剖面流速分布规律,首先分别在不同曝气量下,截取反应器长度方向上的中部及四分之一等分点纵向截面作为分析对象。如图6所示,气水比15∶1和20∶1的速度分布规律与10∶1时相近,且同一气水比条件下3个截面的流速分布规律相似。不同位置截面均呈现流速较高,而两侧区域流速较低的情况。这说明气泡上升过程横向扩散有限,不能有效携带膜片两侧区域的水随其一起运动。同时,气液混合流的集中趋势不利于对膜面的全面冲刷,且由于气泡在上升过程中的浮力作用,水流在反应器顶端的速度越来越快。随着曝气量增大,各截面的最大流速增大。
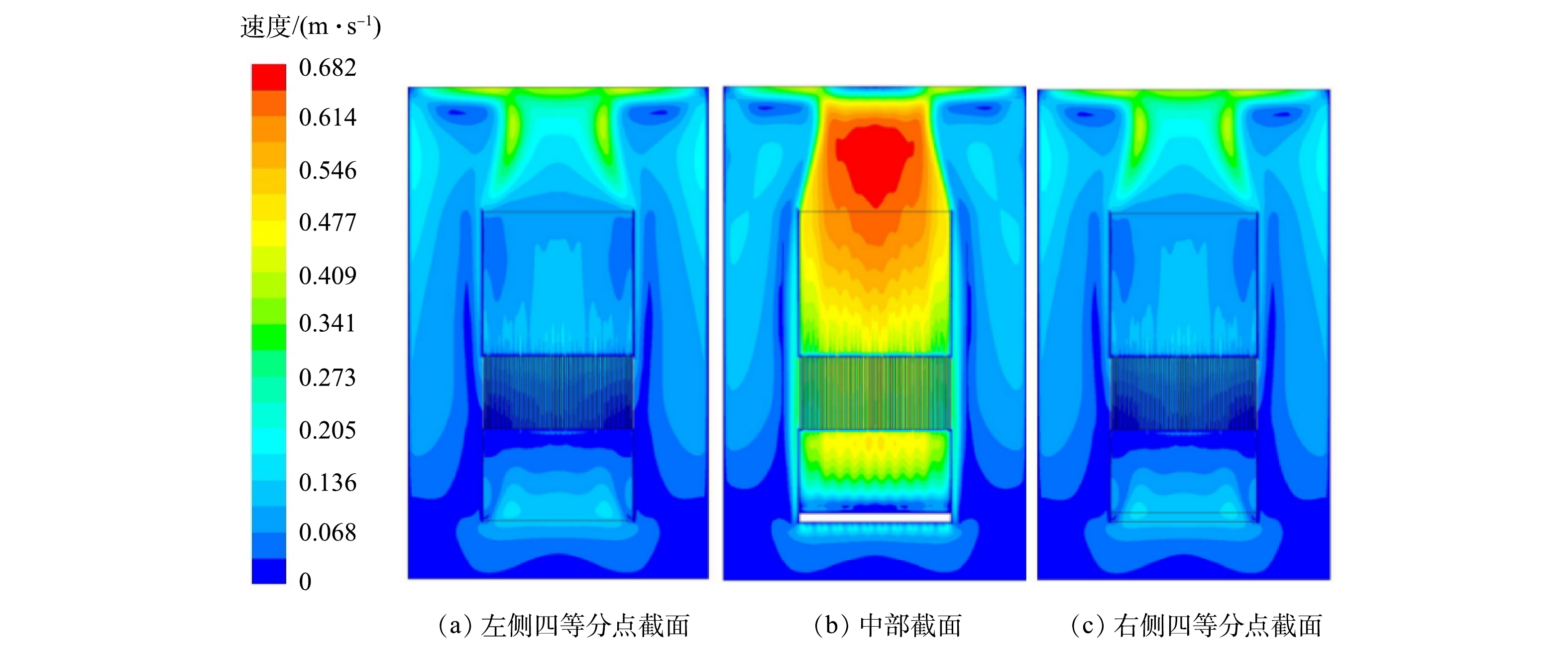
当气水比10∶1时,图7为模拟得到的反应器在宽度方向上不同位置的纵向剖面流速分布结果。3个截面分别位于反应器中部和左、右两侧的四分之一等分点。其中,中间截面正好处在曝气管位置,可以发现比较清晰的高、低速度区域分界面,中间截面流速较高。在膜片区域流速分布基本均匀,而两侧截面流速分布较为相似,流速均较低。这种结果说明了气泡从曝气管中脱离后,进入膜堆的中心位置的速度明显高于进入两侧的速度,导致气泡对膜面中心位置的冲刷能力更强。其次,膜反应器流速沿反应器高度方向逐渐增大,这是由于随着高度增加,液体压力减小,气泡尺寸增大,流体中气相体积分数增大,流速加快,且水流携带能力增强,导致水流速度也相应加快。在膜堆区域,在中间截面部分可以较为明显地看出气泡与膜接触时速度减慢,此时气泡发生了分裂,因此,存在着一定的横向扩散,但左右两侧均有部分空气泡从反应器外侧向上流动,没有充分利用曝气冲刷膜表面的效果。
-
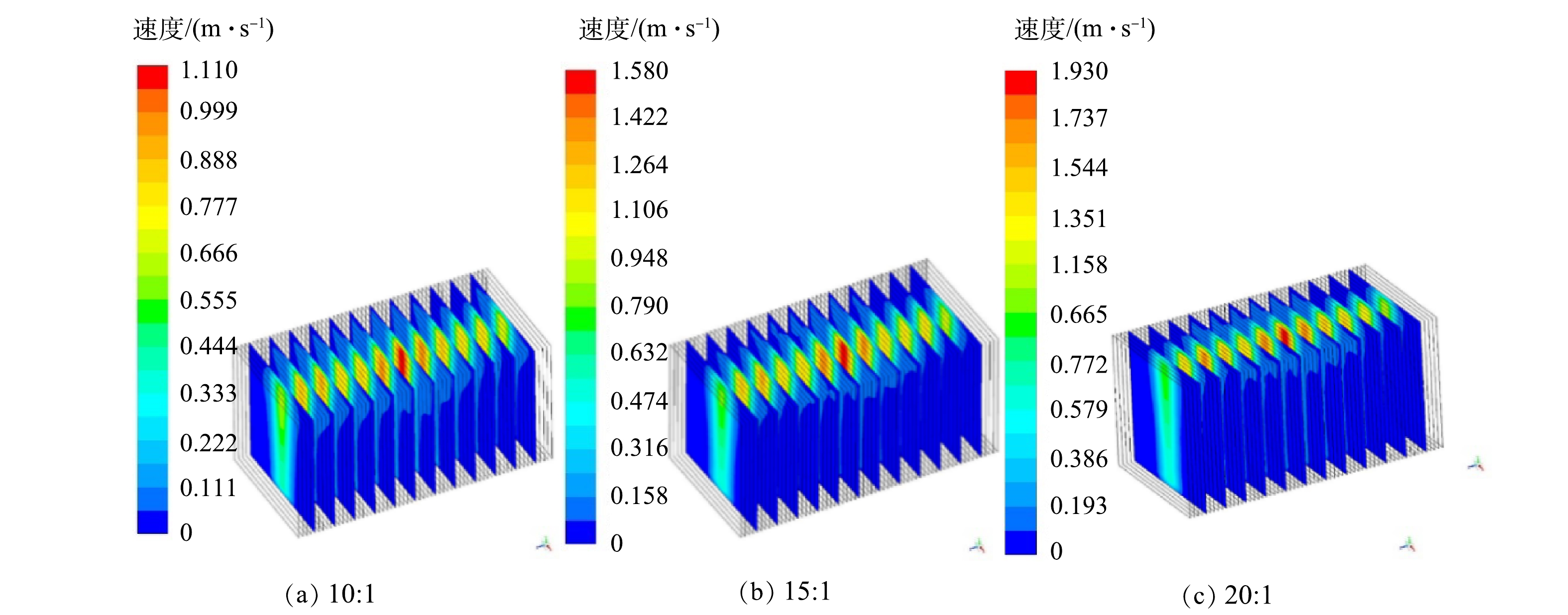
由图8可以看出,在3种气水比条件下的膜片之间的流道内,均呈现中间流速大、两侧流速小的特点。为有效抑制膜片两侧较严重的膜污染现象,可适当改进曝气方式,将单根曝气管换成两根曝气管,其曝气孔的角度由垂直向上分别改为自垂直方向向左、向右偏离45度,使膜面流速分布更加均匀,进一步减少膜面的泥饼层污染现象。这说明膜面两侧区域未能得到有效冲刷,容易形成污泥沉积。此外,反应器中部膜间流道内的流速明显高于两侧膜片间的流速。
为了进一步研究膜间流道的流速分布规律,对不同气水比工况下的膜间流速分布的面积占比进行了分析计算,结果见图9。由于0.1 m · s−1为减轻浓差极化污染的临界错流速率[19],因此以该速度作为划分高低流速区的依据。由图9可看出,角区大多为低速区(<0.1 m·s−1),随曝气量增加,高速区占比相对较为平均且逐渐增大,但整体的分布规律未出现明显变化,可见增加气水比不能有效改变各通道内的流速分布。通过计算,当气水比为10∶1、15∶1、20∶1时,膜间流速小于0.1 m·s−1的区域分别占总面积的61.9%、53.6%、49.6%。气水比由10:1增加到15∶1时,流速低于0.1 m·s−1的区域减少了8.3%;气水比由15∶1增加至20∶1时,相应区域面积占比减少了4%,且减少的趋势放缓。结合曝气能耗,发生上述现象可能的原因是在反应堆的转角不可避免地产生涡流,与主流发生碰撞摩擦,导致部分空气动力能量衰减。因此,在现有的曝气方式下建议采用气水比15∶1进行曝气,以实现气泡对膜片的均匀冲刷。
-
膜面剪切力不仅直接受到液体流速的影响,使膜污染速率发生改变,而且能够反映曝气对膜片表面粘附污泥的清除作用,因此,有必要量化膜面剪切力。由图10可以看出,壁面剪切力分布与膜间流道的流速分布规律相似,中部流速高的区域剪切力大,两侧流速小的区域剪切力小。在膜片底部区域附近,高、低剪切力区域分布界限明显且呈间隔分布。对应气泡冲刷位置的剪切力较高,且随高度增加从两侧向中心汇聚,气泡冲刷效果增强,膜片顶部附近形成高剪切力分布区域,而较小的剪切力是由上升气泡尾部的尾迹产生的,远离膜表面的气泡产生相对较低但恒定、连续的剪切力。以上结果说明膜表面受力不均匀,在膜片两侧容易产生较严重的膜污染。造成该现象的原因可能有曝气孔的数量不足、曝气孔间距较长或曝气管与膜片间距较短。
为了更直观地分析膜面剪切力分布情况,将膜堆中单个膜元件的左右两侧膜面分别记作一个编号,共计128个编号,并计算膜面剪切力的平均值。由图11可看出,不同气水比条件下剪切力平均值变化趋势相近。当气水比由10∶1增加至15∶1时,膜片表面的平均剪切力增大,而气水比由15∶1增加至20∶1时,剪切力增势放缓,进一步验证了15∶1为最优气水比。两侧膜片由于壁面效应及部分空气外溢,流速较低,对应的膜面剪切力也比较低;而中间部分的膜片表面剪切力相对较高,其值较为平均。结合流速分布特性可以发现,膜面剪应力最高的位置与速度增加更强烈的位置一致,说明MBR中流态特征与膜面剪切力分布密切相关。
-
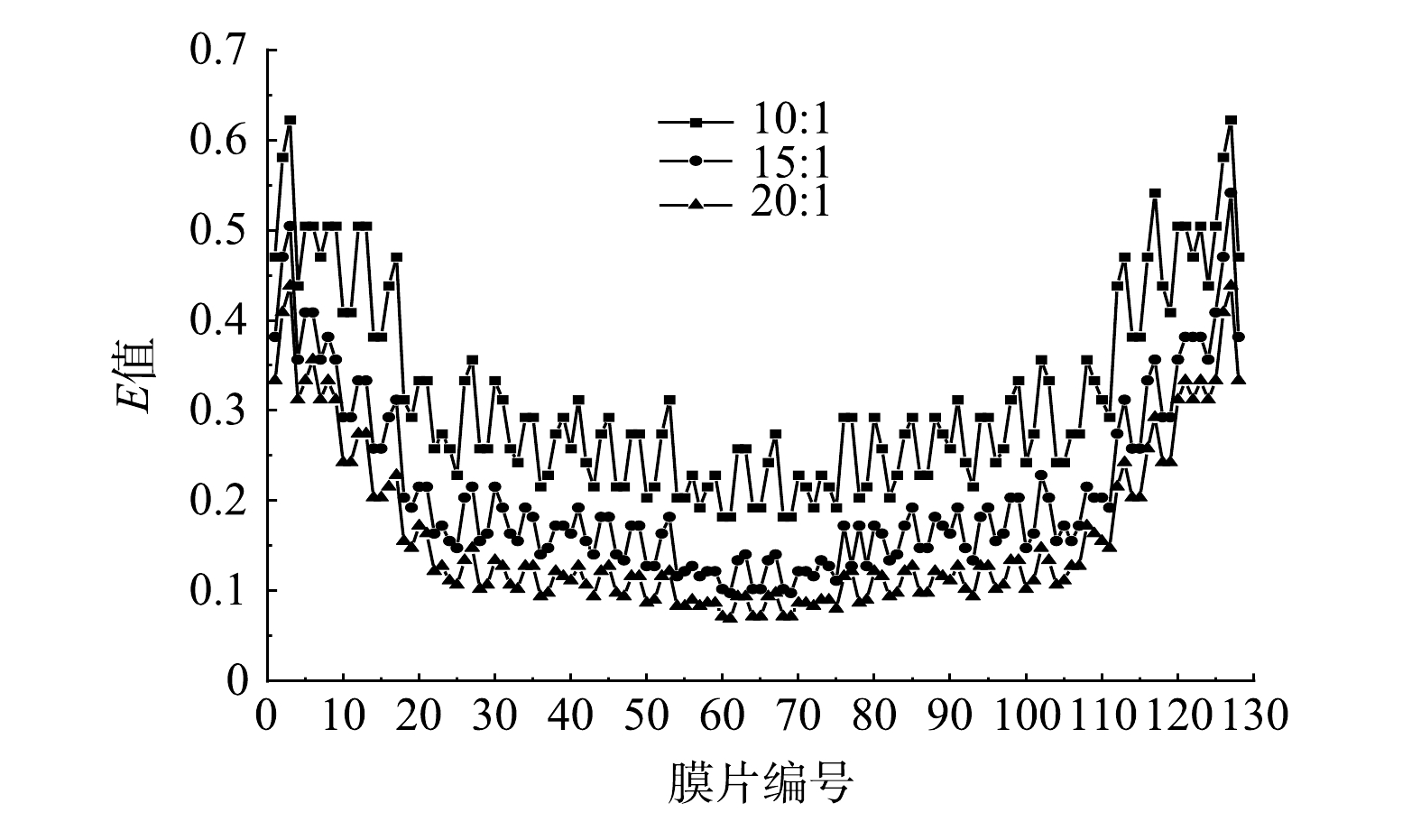
由于控制亚微米级颗粒的沉积不简单依赖于膜面流速的增加,故不予考虑颗粒粒径小于1 μm的情况,且因MBR中微米级颗粒的平均粒径一般为40 μm[16],所以选择40 μm为粒径上限进行计算,结果见图12。图12反映了不同气水比条件下,膜面沉积1~40 μm颗粒的可能性。可以看出,3种气水比条件下的E值均呈现中间低两侧高的现象,即两侧膜面颗粒沉积的概率更大,致使膜污染问题出现的可能性更大,且随曝气量增加E值有所下降。将图12中E值的结果与图11进行对比,发现两者呈现负相关性。膜面剪切力越大则颗粒沉积概率越小;同时,随曝气量增加,膜面剪应力不均匀性更加明显。进一步计算得到,E值大于0.5且极易发生颗粒沉积的膜面积占比分别为12%、2%、0,但当气水比由15∶1增至20∶1时,E值下降程度并不明显,说明在既定的3种气水比条件下,15∶1可以作为最优气水比运行。因此,适当增大剪应力有利于降低膜面颗粒沉降可能性,可通过改变两相流流态,如利用活塞流尾迹区的高值剪应力[25-26],增大气泡对膜面的冲刷覆盖面积,或增大部分区域的湍流程度从而减少死区[27]。
-
1) CFD的模拟结果表明,由于超薄平板膜MBR不同位置处的水流流速及气泡冲刷效果存在差异,各膜片之间的流速分布均存在“中间流速大、两侧流速小、角区低速”现象较为显著的特点,使膜面两侧区域未能得到有效冲刷,易形成膜污染。
2)分析不同气水比条件下流速与膜面平均剪切力的变化趋势,发现随着气水比的增加,膜面平均剪切力呈增大趋势,但当气水比由15∶1增加至20∶1时,膜面平均剪切力的增长趋势变缓。因此,考虑曝气能耗,确定MBR的最优气水比为15∶1。
3) 采用E值表征膜面颗粒沉积概率,发现膜面剪切力均值与E值具有一定负相关性。膜面剪切力均值越大,E值越小,膜面受污染的可能性越小。
4) 根据流态模拟结果,可适当改进MBR的曝气方式,将单根曝气管换成两根曝气管或改变曝气孔角度。
基于CFD的超薄平板膜MBR流态模拟及优化分析
CFD based-flow pattern simulation and optimization analysis of ultra-thin flat membrane MBR
-
摘要: 随着MBR的广泛应用,为控制膜污染导致高运行成本问题,优化新型平板膜MBR的曝气条件成为目前的一个研究热点。本研究通过使用CFD Fluent软件,结合多相流模型和湍流模型进行超薄平板膜MBR的高质量流态模拟,量化膜面剪切力,并从流场及膜污染角度分别对3种气水比(10∶1、15∶1和20∶1)工况下的MBR进行了优化分析,选择出超薄平板膜MBR的最优气水比。研究结果表明,膜片之间的流速分布均存在中间大、两侧小的不均匀性,且单个膜面剪切力分布与MBR流态特征密切相关,膜面颗粒沉积概率与剪切力均值呈负相关;对比了以0.1m·s-1为临界流速的不同曝气下的流场形态分布特性,并综合考虑曝气能耗及膜面冲刷,确定3种气水比中的最优值为15∶1。Abstract: With the wide application of MBR, the problem of high operating cost caused by membrane fouling is becoming more and more prominent. Therefore, optimizing the aeration conditions of new flat membrane MBR has become a research hot spot. In this study, the CFD Fluent software was used to simulate the high-quality flow pattern of the ultra-thin flat membrane MBR combined with the multi-phase flow model and the turbulence model. The membrane surface shear force was quantified, and the MBR operation at three gas-water ratios (10∶1, 15∶1 and 20∶1) was optimized and analyzed from the perspectives of flow field and membrane fouling, so as to select the optimal gas to water ratio of the ultra-thin flat membrane MBR. The results show that the flow velocity distribution between the membranes presented an uneven characteristic of large in the middle and small in both sides, and the shear force distribution on a single membrane surface was closely related to the flow pattern characteristics of MBR. The deposition probability of particles on the membrane surface was negatively correlated with the mean shear force. The flow field distribution characteristics under different aeration conditions with 0.1 m·s−1 critical flow rate were compared. Considering the aeration energy consumption and membrane surface erosion, the optimal gas-water ratio was determined as 15∶1 among above three ratios.
-
-
表 1 超薄平板膜与传统平板膜特性对比
Table 1. Comparison of characteristics between ultra-thin plate membrane and traditional plate membrane
膜类型 装填密度/(m2·m−3) 运行成本 单片厚度/mm 反冲洗 反洗过程是否抖动 常规平板膜 55 高 5~7 否 否 超薄平板膜 90 低 1.2 是 是 -
[1] PAWEL K, LANCE L, SIMOS M, et al. Membrane bioreactors: A review on recent developments in energy reduction, fouling control, novel configurations, LCA and market prospects[J]. Journal of Membrane Science, 2017, 527: 207-227. doi: 10.1016/j.memsci.2016.12.010 [2] 唐婷婷, 张园园, 张佳琳, 等. 新型MBR平板膜及膜堆研究进展[J]. 浙江化工, 2020, 51(10): 51-54. doi: 10.3969/j.issn.1006-4184.2020.10.011 [3] ZHANG J H, XIN Q P, LI X, et al. Mixed matrix membranes comprising amino silane-functionalized graphene oxide for enhanced CO2 separation[J]. Journal of Membrane Science, 2019, 570: 343-354. [4] DE S K, DOTREMONT C, GENNE I, et al. The use of nanoparticles as alternative pore former for the production of more sustainable polyether sulfone ultrafiltration membranes[J]. Journal of Membrane Science, 2014, 471: 168-178. doi: 10.1016/j.memsci.2014.06.061 [5] MAHOUNI A, YLITERVO P, DOYEN W, et al. Continuous bioethanol fermentation from wheal straw hydrolysate with high suspended solid content using an immersed flat sheet membrane bioreactor[J]. Bioresource Technology, 2017, 241: 296-308. doi: 10.1016/j.biortech.2017.05.125 [6] YIANG F, YING Z, YONG F, et al. Fabrication of reactive flat-sheet ceramic membranes for oxidative degradation of ofloxacin by peroxymonosulfate[J]. Journal of Membrane Science, 2020, 611: 118-302. [7] HE L, WANG Y, ZHOU T, et al. Enhanced ammonia resource recovery from wastewater using a novel flat sheet gas-permeable membrane[J]. Chemical Engineering Journal, 2020, 400(15): 125-338. [8] LIU X F, WANG Y, SHI Y R, et al. CFD modelling of uneven flows behavior in flat-sheet membrane bioreactors: From bubble generation to shear stress distribution[J]. Journal of Membrane Science, 2018, 570: 146-155. [9] 王福军. 计算流体动力学分析: CFD软件原理及应用[M]. 北京: 清华大学出版社, 2004. [10] 柳蒙蒙, 陈梅雪, 杨敏, 等. 基于CFD的大型膜生物反应器的设计及运行优化[J]. 环境工程学报, 2018, 12(2): 552-558. doi: 10.12030/j.cjee.201708022 [11] LIU M M, YANG M, CHEN M X, et al. Numerical optimization of membrane module design and operation for a full-scale submerged MBR by computational fluid dynamics[J]. Bioresource Technology, 2018, 269: 300-308. doi: 10.1016/j.biortech.2018.08.089 [12] 郁达伟, 魏源送, 郑祥, 等. 多相流和湍流模型对平板膜生物反应器模拟的影响[J]. 化工学报, 2014, 65(S1): 377-385. [13] YANG M, WEI Y, ZHENG X, et al. CFD simulation and optimization of membrane scouring and nitrogen removal for an airlift external circulation membrane bioreactor[J]. Bioresource Technology, 2016, 219: 566-575. doi: 10.1016/j.biortech.2016.07.139 [14] YANG M, YU D, LIU M, et al. Optimization of MBR hydrodynamics for cake layer fouling control through CFD simulation and RSM design[J]. Bioresource Technology, 2016, 227: 102-111. [15] WANG B, ZHANG K S, FIELD R W. Slug bubbling in flat sheet MBRs: Hydrodynamic optimization of membrane design variables through computational and experimental studies[J]. Journal of Membrane Science, 2017, 548: 165-175. [16] 张晴, 樊耀波, 魏源送, 等. 气升循环分体式MBR的CFD模拟及优化[J]. 膜科学与技术, 2013, 33(4): 107-119. doi: 10.3969/j.issn.1007-8924.2013.04.020 [17] BRAAK E, ALLIET M, SCHETRITE S, et al. Aeration and hydrodynamics in submerged membrane bioreactors[J]. Journal of Membrane Science, 2011, 379(1/2): 1-18. [18] 朱红钧. FLUENT 12 流体分析及仿真[M]. 北京: 清华大学出版社, 2014. [19] RADAEI E, LIU X F, TNG K H, et al. Numerical and experimental investigation of pulse bubble aeration with high packing density hollow-fibre MBRs[J]. Water Research, 2019, 160: 60-69. doi: 10.1016/j.watres.2019.05.056 [20] WANG Y, BRANNOCK M, COX S, et al. CFD simulations of membrane filtration zone in a submerged hollow fibre membrane bioreactor using a porous media approach[J]. Journal of Membrane Science, 2010, 363(1-2): 57-66. doi: 10.1016/j.memsci.2010.07.008 [21] WANG Z W, WU Z C, YIN X, et al. Membrane fouling in a submerged membrane bioreactor (MBR) under sub-critical flux operation: Membrane foulant and gel layer characterization[J]. Journal of Membrane Science, 2008, 325(1): 238-244. doi: 10.1016/j.memsci.2008.07.035 [22] LAY H T, CHEW J W. Critical flux of colloidal foulant in microfiltration: Effect of organic solvent[J]. Journal of Membrane Science. 2020, 616: 118-531. [23] LU X Y, LIU C, HU G Q, et al. Particle manipulations in non-Newtonian microfluidics: A review[J]. Journal of Colloid and Interface Science, 2017, 500: 182-201. doi: 10.1016/j.jcis.2017.04.019 [24] 张宇, 吴志超, 藏莉莉, 等. CFD在平板膜MBR设计及运行优化中的研究[J]. 环境工程学报, 2016, 10(2): 735-741. doi: 10.12030/j.cjee.20160235 [25] LIU X F, WANG Y, SHI Y R, et al. CFD modelling of uneven flows behaviour in flat-sheet membrane bioreactors: From bubble generation to shear stress distribution[J]. Journal of Membrane Science. 2019, 570-571: 144-455. [26] DU X, LIU X F, WANG Y, et al. Particle deposition on flat sheet membranes under bubbly and slug flow aeration in coagulation-microfiltration process: Effects of particle characteristic and shear stress[J]. Journal of Membrane Science, 2017, 541: 668-676. doi: 10.1016/j.memsci.2017.07.023 [27] LIU X F, WANG Y, WAITE T D, et al. Numerical simulations of impact of membrane module design variables on aeration patterns in membrane bioreactors[J]. Journal of Membrane Science, 2016, 520: 201-213. doi: 10.1016/j.memsci.2016.07.011 -


 下载:
下载: