-
《大气污染物综合排放标准》 (GB16297-1996) (后简称“标准”) 规定了等效排气筒的概念。即两个排放相同污染物的排气筒，若其距离小于其几何高度之和，应合并视为一根等效排气筒。若有3根以上的近距排气筒，且排放同一种污染物时，应以前两根的等效排气筒，依次与第三、四根排气筒取等效值”[1]。该标准通过将排气筒的源强叠加、几何高度求均方根平均值的方法得到等效排气筒。等效排气筒为实际工程污染排放的总量核算工作带来了很大便利，而在大气污染运移扩散计算方面尚未进行有效应用。此外，对于多个相近排气筒排放的同一污染物，仍采用繁琐的单个排气筒浓度场叠加的处理方法，如果能利用等效排气筒进行预测评价工作，将为大气污染物的预测计算工作带来很大便利。
高斯扩散模式 (Gauss模式) 及其变形作为大气污染研究的基本模型，在高架点源和地面点源大气污染物运移扩散方面具有广泛应用 [2-4]。MOK等[5]利用改进的高斯烟羽模型探究了非均匀风条件下SO2的扩散情况，通过与实测数据进行对比，验证了复杂风场下高斯模式用于预测污染物迁移扩散的合理性。程穆阳[6]利用修正后的高斯点源扩散模型对多点源污染物的扩散浓度分布特征进行了探究，结果表明污染物浓度分布趋势与实际值基本一致，但模型的预测精度仍有待进一步提升。同时，目前对于等效排气筒能否用于大气环境影响的预测还存在一定争议[7]，主要是预测精度和范围的实际情况不明确。
等效排气筒预测应用的关键是要解决等效后相关参数计算方法的可行性问题，并验证其等效预测结果的合理性[8-9]。现行标准中仅对等效排气筒的污染物排放速率 (算术叠加) 及等效几何高度 (均方根平均) 进行了规定，而尚未提及预测计算中高斯模式所需其他参数 (如烟气温度Ts、抬升高度ΔH等) 的等效计算方法，这大大限制了等效排气筒概念的拓展应用。因此，如果能综合考虑排气筒高度、排放源强以及风速等因素的影响，提出一种既能满足总量控制、又能用于下游污染水平预测的等效排气筒参数计算方法，将为标准中等效排气筒的拓展应用提供参考。
本研究在满足总量控制要求的基础上，从等效排气筒参数的计算方法入手，采用典型案例分析比较相近排气筒等效前后下风向地面浓度场的差异性，探索几种典型计算方法用于等效排气筒参数计算的可行性和合理性，筛选可采用高斯模式预测计算的等效排气筒参数的有效计算方法，以期拓展等效排气筒概念在大气预测评价工作中的应用。
-
在某农村地区，大气稳定度主要为D，常年平均大气温度Ta=293.15 K，大气压Pa=1 000 hPa，当地多年平均风速U10为3.5 m·s−1，混合层高度ha大于200 m。某企业的2条生产线分别建有1根排气筒，相对位置如图1所示。排气筒底部中心坐标分别为 (0, –D/2) 和 (0, D/2) 。该企业周边5 km范围内未见较高地形地貌和构筑物。两排气筒的几何高度[10]分别为H1和H2，且都大于15 m，并满足H1+H2>D。两排气筒的烟气排放量分别为Q1和Q2；烟气中SO2质量浓度分别为C1和C2；出口半径分别为r1和r2；出口处烟气温度分别为Ts1和Ts2；烟气热释放率分别为Qh1和Qh2；烟气抬升高度分别为ΔH1和ΔH2；烟云有效高度分别为He1 (=H1+ΔH1) 和He2 (=H2+ΔH2) 。该企业运行期每年运行350 d，2条生产线不间断连续运行，排气筒的烟气排放速率及污染物质量浓度稳定。
-
根据评价范围选取原则，将下风向计算范围设定为域Ω (0≤x≤25 000 m，–4 000≤y≤4 000 m) 。高斯扩散模式中考虑地面反射的下风向地面任一点 (x, y, 0) 的污染浓度值C计算公式见式 (1) 。
式中：C为污染物浓度，μg·m−3；W为污染物质量排放速率，μg·s−1；σy为水平方向扩散参数，m；σz为垂直方向扩散参数，m；x、y分别为计算点与烟囱底部中心的相对距离，m；U为排气筒出口高度处的平均风速，m·s−1；He为烟气排放有效高度，m。其中，扩散参数
$ {\sigma }_{y}={\gamma }_{1}{x}^{{\alpha }_{1}} $ 、$ {\sigma }_{z}={\gamma }_{2}{x}^{{\alpha }_{2}} $ ，在大气稳定度为D的情况下，回归指数α1、γ1、α2、γ2的值取自P-G扩散曲线[11] (表1) ，与排气筒下游相对距离有关。假设距离地面10 m高处的风速为u，则排气筒口处的风速用公式
$ U=u{\left({Z}_{2}/{Z}_{1}\right)}^{p}{，Z}_{2}\leqslant 200m $ ；$ U=u{\left(200/{Z}_{1}\right)}^{p}，{Z}_{2}＞200m $ 计算。在大气稳定度为D的乡村，p取0.15[11]。 -
根据标准规定及总量控制要求，等效排气筒烟气排放速率Q=Q1+Q2；污染物质量排放速率W=W1+W2= Q1C1+ Q2C2。参照标准规定，首先将等效排气筒的几何高度和烟气抬升高度ΔH进行等效计算，随后求出烟气排放的有效高度He。
等效的概念主要是基于一种代表性平均值的思路，分为简单平均法和加权平均法两大类。表2列出了常见的多种等效平均值求解方法。其中，方法1~4为简单平均值、方法5~8为方法1~4对应的加权平均值。再通过应用高斯模式比较分析其预测结果的可行性和合理性，并筛选出有效的参数等效方法。
首先，以低矮点源排气筒为例[12]，设定A、B两组等效前排气筒参数 (表3) ，采用标准中推荐的均方根平均法 (表2) 对等效前 (即分开计算两根排气筒下风向地面浓度场后叠加所得地面浓度场[13]) 和等效后 (即计算一根等效排气筒下风向地面浓度场) 的浓度场分布进行高斯预测，分析评估均方根平均法的有效性。其次，进一步对其他平均法 (表2) 等效前后下风向浓度场的分布进行比较，得出相对较优的等效排气筒参数计算方法。最后，通过设定两根排气筒的差异性烟气排放量 (Q) 或排放浓度 (C) ，以及差异性风速条件 (U) 等[14-15]，分析所得等效排气筒与相应等效前下风向地面浓度场分布的差异性，进一步论证所得等效方法的合理性及适用性。
-
分别将A组 (H1=H2=50 m、Q1=Q2=20 000 m3·h−1) 、B组 (H1=50 m、H2=30 m、Q1=20 000 m3·h−1、Q2=10 000 m3·h−1) 数据按照表2中的方法4 (均方根平均法) 进行计算，发现等效前后排气筒下风向污染物的浓度场分布特征基本一致 (图2) 。表4汇总了等效前后下风向地面等浓度线的覆盖面积及其差异。
在最大落地浓度位置方面，A组等效前、后的位置分别在下风向坐标(1 291 m, 0 m)和 (1 239 m, −8 m)处，B组则分别在(965 m, 7 m) 和(999 m, −8 m)处，A组等效后比等效前最大落地浓度点更靠近于排放源。在最大落地浓度值方面，A组等效前、后分别为6.913 μg·m−3和7.228 μg·m−3，相对误差为−4.56%；B组则分别为8.078 μg·m−3和8.859 μg·m−3，相对误差为9.67%。此外，在等浓度线为2.5 μg·m−3时，A组的污染覆盖面积相对误差即可小于1% (图2(a)) ，B组仍为4.22% (图2(b)) ，并且随着排气筒下风向距离的增加精确度会相应提升。
A、B两组的等效结果显示了方法4不同的预测精度，采用等效排气筒预测的结果受等效前排气筒高度和源强等参数的影响，即方法4对于相同参数的排气筒具有更好的等效预测结果。同时，等效前、后浓度场的主要差异体现在排气筒下风向等浓度线5 μg·m−3的范围内，而最大落地浓度点也在此范围内。
基于等效前后等浓度线和最大落地浓度点处浓度的比较分析，发现采用标准中推荐的均方根法 (方法4) 来进行ΔH的等效计算后，对于距离排气筒较近的最大落地浓度点的相对误差较大，不符合预测要求。因此，有必要遴选一种更精确的等效参数计算方法用于预测计算。
-
采用2.1的方法对表2中其他7种等效方法进行等效计算并与等效前进行比较。其中，等效前排气筒参数设置同B组。7种等效方式与均方根法获得的下风向地面浓度场分布趋势相似 (图3) ，但各等浓度线覆盖面积的差异仍较大 (表5) 。
总体而言，7种等效方式对等浓度线覆盖面积的预测误差相较于等效前，主要集中在5 μg·m−3、2.5 μg·m−3两条等质量浓度线内。而在5 μg·m−3等质量浓度线内，4种加权等效方式 (方法4~8) 的相对误差显著小于不加权方式。其中，方法6和7与等效前最为接近，误差分别为7.75%和-10.21%。在2.5 μg·m−3等质量浓度线内，方法1、2的误差仍较大，而其他5种方法的相对误差可控制在10%以内。此外，方法7所得的等质量浓度线覆盖面积均小于等效前。在等质量浓度线为0.25 μg·m−3处的相对误差低于1%，而方法6则在等质量浓度线1 μg·m−3处相对误差小于1%。
对于最大落地质量浓度的预测，7种等效方式的最大落地质量浓度位置均集中在1 000 m附近 (表6) 。其中，方法6~8的最大落地质量浓度预测误差小于方法4。尤其是方法7的误差，仅为2.70%，展现了更好的预测效果。此外，由标准中y值计算公式得到的7种等效方式所获得最大落地质量浓度点的y坐标均为−8 m，而等效前该值为7 m。两值的符号相反，表明产生了较大偏差。
综上所述，方法6、7对下游污染物质量浓度及其范围的预测，相较于方法4预测精度更高。后续将进一步对比这3种公式的预测效果。
-
由2.1可知，等效前排气筒参数的改变对于等效预测的结果影响显著，而源强作为排气筒的重要参数[16]，因此，有必要探究其对等效预测结果的影响。此外，由于排气筒对下游的污染主要集中在坐标原点附近的下游地区，故后续将重点关注坐标原点到下游25 km范围内的污染物分布情况。
通过改变表3中B组Q1的数值，得到不同源强比W1=0.5W2、W1=W2、W1=3W2。将方法4、6、7在不同排放速率下的预测结果汇总于图4中，其关键点数据见表7。由高斯公式 (式 (1) ) 可知，在排放质量浓度C不变的条件下，总源强W与Q呈正相关，因而随着Q不断增大，总源强不断增大，等效前最大落地质量浓度由6.189 μg·m−3增至8.887 μg·m−3，等效前最大落地质量浓度点也由800 m相应增至1 010 m。当W1<W2时，由于方法4相较于方法6、7的有效高度大，故其预测污染浓度显著偏小；而当W1＞W2时，预测结果则恰好相反。
分析等效后预测污染浓度值与等效前的关系，发现采取源强加权的方法6和7的等效排气筒受W比值变化影响较小，与等效前污染浓度值的关系相对稳定且接近。在最大落地质量浓度点处，方法7的预测浓度与等效前浓度较接近，误差随着源强比的增大而增大，但始终在5%以内。而方法4的最大落地质量浓度随源强比改变发生显著变化，相较于等效前产生了很大偏离，在W1=W2处获得最小误差7.02%，预测精度较差。
而对于预测范围，在整个0~25 km，无论源强比如何变化，方法4不存在预测误差小于1%的情况，而方法6和7均可使预测误差小于1%。其中，方法7在2 400 m后相对误差均小于1%，相应的预测精度最高。
综上所述，标准中使用的方法4不能保证源强变化条件下的预测稳定性，故应寻求一种更稳定的等效高度计算方式。方法7的预测精度高，且受源强改变的影响较小，故进一步验证方法7在不同工况下的预测效果。
-
风速是重要的环境因素，会显著影响高斯模式预测的结果[17-18]。因此，有必要验证不同风速条件下方法7预测模型的有效性。保持其他参数与2.2相同，设置10 m处风速u的不同取值，得到方法7的质量浓度预测结果如图5所示，关键点数据见表8。
改变风速条件，地面预测质量浓度与等效前基本保持了较好的一致性，且始终略低于等效前的值。其中，最大落地质量浓度受影响程度最大。当风速为4.5 m·s−1时，最大落地质量浓度预测值与等效前的相对误差最小，为2.21%；随着风速逐渐减至1.5 m·s−1，预测值与等效前值的误差则不断增大至6.87%，但仍可满足等效预测所需的精度要求。同时，等效前后最大落地质量浓度点的位置也受风速条件的影响，最大落地质量浓度点离坐标原点的距离随风速增大有所减小。当u=1.5 m·s−1时，等效前后最大落地质量浓度点的位置相差最大，绝对误差为180 m；当u=3.5 m·s−1时，二者相差最小，为5 m。这主要是由于等效后相较于等效前最大落地距离对风速的响应更为明显。
此外，改变风速对方法7的预测范围及精度存在一定影响 (见表8) 。当风速增大时，相对误差小于1%和10%水平的预测范围不断增大，等效后质量浓度与等效前接近，预测效果增强。而下风向5 000 m处的地面质量浓度误差作为等效排气筒预测的重要考核指标，方法7在该处仅表现出约2‰的相对误差，显示出很好的预测效果。综上所述，无论风速如何变化，方法7的预测模式都很好地拟合了等效前的污染物浓度水平，表现出很强的预测稳定性和连续性，且风速越大该模式的预测精度越高。
-
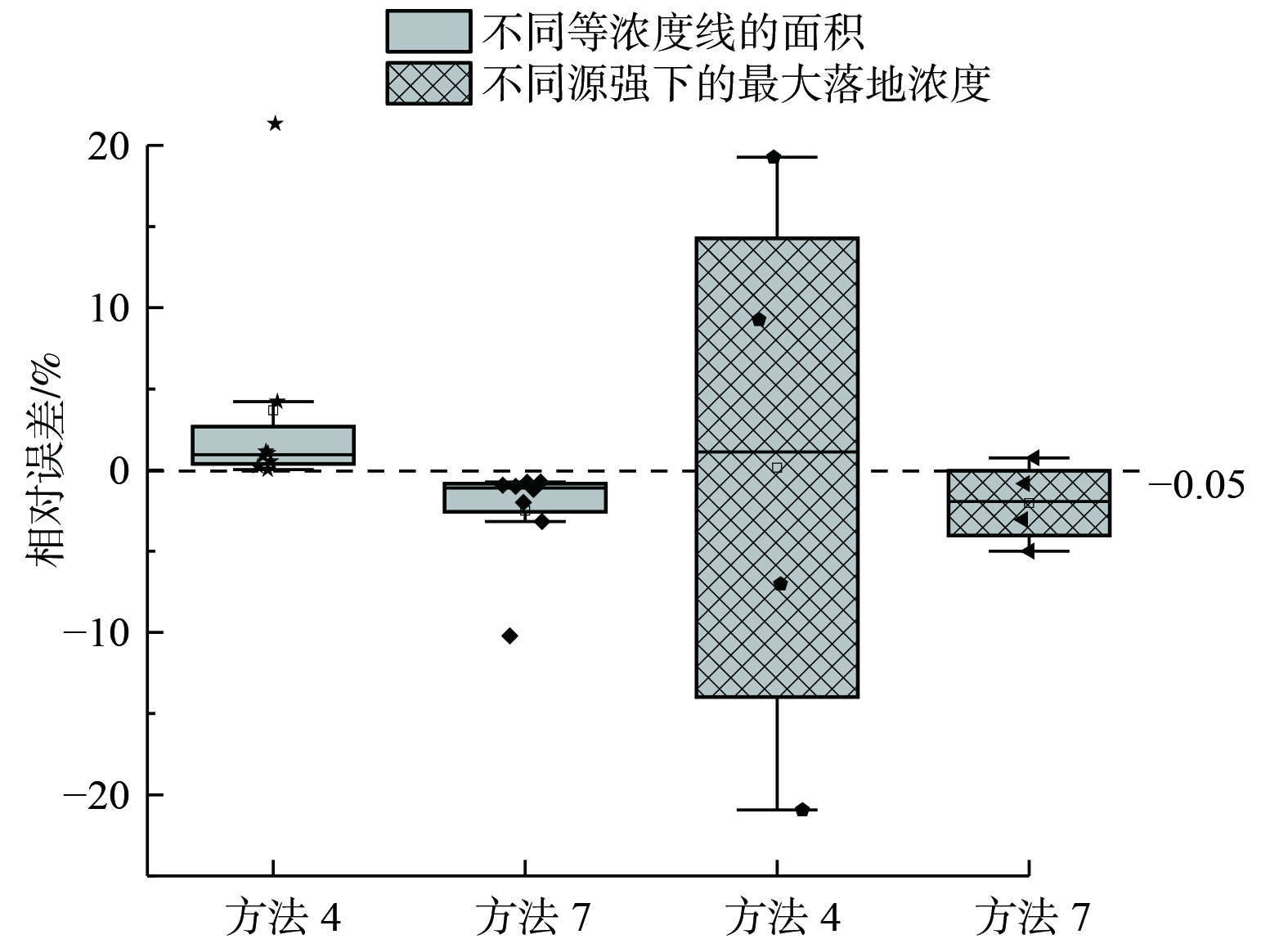
基于上述等效排气筒的预测结果，探讨了将源强加权算术平均法用于等效预测的可行性，并与现行标准中均方根平均法进行了比较 (如图6所示) 。等效前排气筒参数相同时，均方根平均法可较好地满足等效预测的范围和浓度需求；而参数不同 (高度或者源强改变) 时，均方根法不再满足预测要求。这是由于高斯公式中等效有效高度He与H1、H2、W1、W2等值均相关，而均方根法并没有考虑源强因素。因此，在源强改变时，其等效预测的最大落地浓度相对误差为−20.94%~19.28%，预测结果会产生较大偏差。此外，多个排气筒计算顺序的改变也会对均方根法的预测结果造成影响[19]，故均方根法只能用于污染物的总量控制。若使用源强加权算术平均法进行等效预测 (相对误差为−5.00%~0.74%) ，不仅可利用其源强稳定性的特点消除排气筒源强变化对预测的影响，且不需要考虑排气筒的计算顺序问题，因此，可更好地应用于大气污染预测中。
源强加权等效预测方式的等质量浓度线覆盖面积明显低于不加权的情况。其中，方法7与方法8所得的等质量浓度线覆盖面积和最大落地质量浓度均小于等效前。这可能是等效得到的有效高度不同而导致。有效高度的增加使得地面污染质量浓度和等质量浓度线覆盖面积相应减小[20-21]。而本研究中涉及的有效高度值从方法4到方法1不断下降，源强加权高度又普遍高于不加权。因此，方法8作为均方根法的加权形式，更高的有效高度及更大的预测范围偏差均会使其不能满足等效预测的精度要求。
风速对于污染物扩散的影响主要表现在下游污染物浓度方面[22]。分析高斯公式可知，下游污染物的质量浓度与风速呈反比，因此，风速的增大有利于下游污染物质量浓度减小且均匀分布。在风速较小时，排放点附近过高的污染物质量浓度导致了等效排气筒在排放点下游近距离处的预测受限[23]。随着风速逐渐增大，污染物进一步扩散[24-25]，等效排气筒的预测误差也不断减小，因此，源强加权算术平均法在风速较大时可实现较高的预测水平。
等效前最大落地质量浓度点的Ym=7 m，等效后Ym=-8 m，即最大落地质量浓度点的y轴位置存在着一定的偏差。这是由于等效后最大落地浓度点的坐标Ym与等效排气筒的y值坐标`y一致，而标准中等效排气筒
$ `y=\mathrm{a}{W}_{2}/W $ 的计算公式仅考虑了源强对等效排气筒位置的影响，却忽略了排气筒高度等因素的作用。由于等效前排气筒到等效排气筒的距离与等效前排气筒高度呈负相关，因此，可在原`y值计算公式的基础上乘以系数H/H1得到公式$ `y=a{(W}_{2}H)/(W{H}_{1}) $ ，亦可将源强和高度等因素加权计算从而获得更加精确的预测结果。高斯模式及其变形是目前常用的环评手段，而等效排气筒尚未有很好地应用。若能将改进的等效排气筒与《环境影响评价技术导则》 (HJ 2.2-2018) [26]中推荐的大气预测估算模型 (如AERSCREEN等[27-28]) 相结合，则能增大估算模型的适用范围，并为大气污染预测提供便利。
-
1) 提出了一种利用源强加权算术平均法进行等效排气筒污染预测的方法，实现了下游污染物浓度和范围的有效预测，同时优化了等效排气筒的高度计算公式，可为大气污染预测评价中等效排气筒的应用提供参考。
2) 提出在不同排气筒高度和源强参数下，源强加权算术平均法相较于其他典型等效计算方法 (包括标准中采用的均方根平均法) 在预测范围和最大落地浓度等方面具有更优的预测精度，且等效后下风向浓度场总体分布趋势与等效前叠加计算结果一致。
3) 源强加权算术平均法在风速改变时保持了很好的预测精度和预测稳定性，特别是在风速较大时其预测精度更高。其中，在风速4.5 m·s−1时，该方法的最大落地浓度预测相对误差仅为−2.21%。
等效排气筒有效高度计算方法的比选及其应用于大气污染预测的可行性
Comparison of methods for calculating the effective height of equivalent exhaust tubes and their feasibility in predictive applications
-
摘要: 目前，等效排气筒多用于大气污染物总量控制，其预测精度和范围的不明晰限制了其在污染物运移扩散领域的进一步应用。基于《大气污染物综合排放标准》，依据所预测的范围和浓度精度对8种典型等效计算方法进行了比选，并验证了将等效排气筒用于不同工况下污染物运移扩散预测的可行性。改进的有效高度等效算法 (源强加权算术平均法) 综合考虑了不同高度和源强参数特征，以2个排放同种污染物的相邻排气筒为例，所计算的高斯模式下等效后下风向污染物浓度场总体分布趋势与等效前叠加计算结果一致，且预测精度优于《大气污染物综合排放标准》中提出的均方根平均法和其他等效算法。对不同风速条件下 (1.5~4.5 m·s−1) 等效前后下风向污染物浓度场分布计算比较，发现即使风速改变仍可保证较高的最大落地浓度预测精度 (−6.87%~−2.21%)，特别是风速较大时其预测精度更高 (达到−2.21%) 。这验证了该方法的有效性和稳定性。本研究探讨的源强加权算术平均值算法，进一步提升了等效排气筒相关参数计算的合理性，并拓展了其在大气预测评价中的应用。Abstract: Equivalent exhaust tubes are currently used mainly for total air pollutant control, and the lack of clarity in prediction accuracy and scope limits its further application in the field of pollutant transport and dispersion. Based on the Integrated emission standard of air pollutants, this study compared and selected eight typical calculation methods according to the predicted scope and concentration accuracy, and the feasibility of using equivalent exhaust tubes for the prediction of pollutant transport dispersion under different working conditions was verified. The effective height equivalence algorithm (source intensity weighted arithmetic averaging method) modified in this paper was used to integrate the different height and source intensity parameter characteristics. Taking two adjacent exhaust tubes emitting the same pollutant as an example, the overall distribution trend of the calculated downwind pollutant concentration field under the Gauss model after equivalence was consistent with the results before equivalence. In addition, the prediction accuracy of this method was better than that of the root mean square averaging method proposed in the Integrated emission standard of air pollutants and other equivalent algorithms. The calculation and comparison of pollutant concentration field distribution in the downwind direction before and after equivalence under different wind speed conditions (1.5~4.5 m·s−1) showed that even if the wind speed changed, it could still ensure a high prediction accuracy of the maximum fallout concentration (−6.87%~−2.21%). Especially, the higher prediction accuracy (−2.21%) at higher wind seeds showed the effectiveness and stability of this method. The use of the source intensity weighted arithmetic averaging method will further improve the rationality of the calculation of the equivalent exhaust-related parameters and expand their application in air prediction and evaluation.
-
-
图 1 2个近距离排气筒及其下风向关心点的相对位置示意
Figure 1. Schematic diagram of the relative positions of two near exhaust tubes and their downwind observation points
图 2 等效前后2个近距离排气筒下风向地面浓度场分布
Figure 2. Distribution of downwind ground concentration field before (above) and after (below) equivalence of two close exhaust tubes
图 3 7种等效方式下2个近距离排气筒的下风向地面浓度场分布
Figure 3. Downwind ground concentration field distribution obtained by seven equivalent methods of two near exhaust tubes
图 4 不同W比值下的等效排气筒预测质量浓度
Figure 4. Predicted concentration of equivalent exhaust tubes under different source intensity ratios
图 5 不同风速下源强加权算术平均法 (方法7) 的等效预测曲线
Figure 5. Equivalent prediction curve of source intensity weighted arithmetic averaging method (Equation 7) under different wind speeds
图 6 不同条件下均方根法 (方法4) 与源强加权算术平均法 (方法7) 的相对误差比较
Figure 6. Comparison of the relative errors of root mean square averaging method (Equation 4) and source intensity weighted arithmetic averaging method (Equation 7) under different conditions
表 1 大气稳定度为D时α1、γ1、α2、γ2的值
Table 1. The values of α1, γ1, α2, γ2 when the atmospheric stability is D
x /m α1 γ1 α2 γ2 0~1 000 0.929 418 0.110 726 0.826 212 0.111 771 1 000~10 000 0.888 723 0.146 669 0.632 023 0.528 992 ＞10 000 0.888 723 0.146 669 0.555 350 0.810 763 
下载: 导出CSV
表 2 典型平均值的计算方法
Table 2. Calculation of typical average values
序号 等效方式 计算公式 等效后几何高度H 等效后抬升高度ΔH 1 调和平均 $ \stackrel{-}{X}=2{X}_{1}{X}_{2}/({X}_{1}+{X}_{2}) $ $ {H}_{1}=2{H}_{1}{H}_{2}/({H}_{1}+{H}_{2}) $ $ {`\Delta H}_{1}=2{\Delta H}_{1}{\Delta H}_{2}/({\Delta H}_{1}+{\Delta H}_{2}) $ 2 几何平均 $ \stackrel{-}{X}=\sqrt{{X}_{1}{X}_{2}} $ $ {H}_{2}=\sqrt{{H}_{1}{H}_{2}} $ $ {`\Delta H}_{2}=\sqrt{{\Delta H}_{1}{\Delta H}_{2}} $ 3 算术平均 $ \stackrel{-}{X}={(X}_{1}+{X}_{2})/2 $ $ {H}_{3}={(H}_{1}+{H}_{2})/2 $ $ {`\Delta H}_{3}={(\Delta H}_{1}+{\Delta H}_{2})/2 $ 4 均方根平均 $ \stackrel{-}{X}=\sqrt{({X}_{1}^{2}+{X}_{2}^{2})/2} $ $ {H}_{4}=\sqrt{({H}_{1}^{2}+{H}_{2}^{2})/2} $ $ {`\Delta H}_{4}=\sqrt{({\Delta H}_{1}^{2}+{\Delta H}_{2}^{2})/2} $ 5 加权调和平均 $ \stackrel{-}{X}={X}_{1}{X}_{2}/({\beta }_{1}{X}_{2}+{\beta }_{2}{X}_{1}) $ $ {H}_{5}=W{H}_{1}{H}_{2}/({W}_{1}{H}_{2}+{W}_{2}{H}_{1}) $ $ {`\Delta H}_{5}=W{\Delta H}_{1}{\Delta H}_{2}/({W}_{1}{\Delta H}_{2}+{W}_{2}{\Delta H}_{1}) $ 6 加权几何平均 $ \stackrel{-}{X}={X}_{1}^{{\beta }_{1}}{X}_{2}^{{\beta }_{2}} $ $ {H}_{6}={H}_{1}^{\frac{{W}_{1}}{W}}{H}_{2}^{\frac{{W}_{2}}{W}} $ $ {`\Delta H}_{6}={\Delta H}_{1}^{\frac{{W}_{1}}{W}}{\Delta H}_{2}^{\frac{{W}_{2}}{W}} $ 7 加权算术平均 $ \stackrel{-}{X}={{\beta }_{1}X}_{1}+{{\beta }_{2}X}_{2} $ $ {H}_{7}=({{W}_{1}H}_{1}+{{W}_{2}H}_{2})/W $ $ {`\Delta H}_{7}=({{W}_{1}\Delta H}_{1}+{{W}_{2}\Delta H}_{2})/W $ 8 加权均方根平均 $ \stackrel{-}{X}=\sqrt{({\beta }_{1}{X}_{1}^{2}+{\beta }_{2}{X}_{2}^{2})} $ $ {H}_{8}=\sqrt{({W}_{1}{H}_{1}^{2}+{W}_{2}{H}_{2}^{2})/W} $ $ {`\Delta H}_{8}=\sqrt{({W}_{1}{\Delta H}_{1}^{2}+{W}_{2}{\Delta H}_{2}^{2})/W} $ 注：β1和β2分别为X1和X2的权重，满足W=W1+W2， $ {\beta }_{1}=\dfrac{{W}_{1}}{{W}_{1}+{W}_{2}} $ $ {\beta }_{2}=\dfrac{{W}_{2}}{{W}_{1}+{W}_{2}} $
下载: 导出CSV
表 3 等效前2个排气筒的设定参数
Table 3. Setting parameters of the two equivalent previous exhaust tubes
组别 y1/m y2/m H1/m H2/m Q1/(m3·h−1) Q2/(m3·h−1) A组 −25 25 50 50 20 000 20 000 B组 −25 25 50 30 20 000 10 000 组别 T1 /K T2 /K D1 /m D2 /m C1 / (mg·m−3) C2/ (mg·m−3) A组 333.15 333.15 1 1 90 90 B组 333.15 333.15 1 1 90 90 注：等效前排气筒的抬升高度采用公式 $ △H=2(1.5{V}_{s}D+0.01{Q}_{h}) /U $
下载: 导出CSV
表 4 等效前后对应等浓度线的覆盖面积及相对误差
Table 4. Coverage and relative error of corresponding concentration lines before and after equivalence
等质量
浓度线/(μg·m−3)等效前覆盖面积/m2 等效后覆盖面积/m2 面积相对误差 A B A B A B 5.00 1.58×105 1.58×105 1.74×105 1.92×105 9.92% 21.34% 2.50 1.19×106 9.26×105 1.20×106 9.65×106 0.39% 4.22% 1.00 5.24×106 3.88×106 5.22×106 3.93×106 −0.30% 1.14% 0.50 1.40×107 1.01×107 1.39×107 1.02×107 −0.25% 1.05% 0.25 3.57×107 2.58×107 3.56×107 2.61×107 −0.18% 0.86% 0.10 5.71×107 5.27×107 5.70×107 5.30×107 −0.14% 0.54% 0.05 6.84×107 6.52×107 6.84×107 6.54×107 −0.13% 0.22% 0.01 8.91×107 8.72×107 8.90×107 8.72×107 −0.12% 0.03%
下载: 导出CSV
表 5 其他7种等效方式所得等质量浓度线覆盖面积与等效前的相对误差
Table 5. Relative error of the area covered by the isoconcentration lines obtained by the other seven equivalence methods compared with that before equivalence
等质量
浓度线/
(μg·m−3)等质量浓度线覆盖面积的相对误差 方法1 方法2 方法3 方法5 方法6 方法7 方法8 5 77.22% 59.71% 40.39% 27.47% 7.75% −10.21% −25.28% 2.5 16.99% 12.88% 8.55% 5.61% 1.07% −3.17% −6.94% 1 7.28% 5.30% 3.19% 1.76% −0.21% −1.99% −3.51% 0.5 5.02% 3.72% 2.37% 1.44% 0.07% −1.19% −2.23% 0.25 3.81% 2.83% 1.82% 1.13% 0.15% −0.75% −1.53% 0.1 0.56% 0.29% 0.0014% −0.20% −0.48% −0.74% −0.97% 0.05 −0.03% 0.201% −0.53% −0.66% −0.84% −1.01% −1.42% 0.01 −0.66% −0.77% −0.88% −0.96% −0.95% −0.93% −1.01%
下载: 导出CSV
表 6 不同等效方式所得最大落地质量浓度及其坐标
Table 6. Maximum landing concentrations and their coordinates obtained by different equivalence methods
等效公式 最大落地点
的坐标/m最大落地
质量浓度/(μg·m-3)相对
误差RE方法1 (889，−8) 11.091 37.30% 方法2 (926，−8) 10.274 27.18% 方法3 (965，−8) 9.517 17.84% 方法4 (1 000，−8) 8.859 9.67% 方法5 (990，−8) 9.065 12.22% 方法6 (1 000，−8) 8.423 4.27% 方法7 (1 000，−8) 7.860 -2.70% 方法8 (1 022，−8) 7.394 -8.47%
下载: 导出CSV
表 7 不同W比值下等效前后下风向关键点的污染物预测质量浓度
Table 7. Predicted pollutant concentrations at key points downwind before and after equivalence under different source intensity ratios
源强比 Y=0 时的最大
落地点距离x/m最大落地质量
浓度/(μg·m−3)相对误差小于1%的
范围/m (x≤25 000)相对误差小于10%的
范围/m (x≤25 000)等效前 公式4 公式6 公式7 等效前 公式4 公式6 公式7 公式4 公式6 公式7 公式4 公式6 公式7 W1=0.5W2 800 950 800 835 6.189 4.893 6.703 6.235 无 >5 500 >2 200 >1 600 >400 >600 W1=W2 865 960 895 925 6.876 6.393 7.303 6.819 无 >6 100 >2 400 >900 >600 >700 W1=2W2 985 1 000 995 1 005 8.046 8.792 8.356 7.800 >12100 >6 700 >1 200 >700 >700 >1 000 W1=3W2 1 010 1 000 1 080 1 135 8.887 10.60 9.106 8.443 无 >7 600 >1 500 >2 400 >800 >1 000
下载: 导出CSV
表 8 不同风速下源强加权算术平均法 (方法7) 等效前后下风向关键点污染物预测质量浓度
Table 8. Predicted pollutant concentrations at key points downwind before and after source intensity weighted arithmetic averaging method (Equation 7) equivalence at different wind speeds
风速/(m·s−1) 最大质量浓度落地点 相对误差 x=5 000 m处的RE RE<1%的范围/m
(x≤25 000 m)RE<10%的范围/m
(x≤25 000 m)距离/m 质量浓度/(μg·m−3) 等效前 公式7 等效前 公式7 1.5 1 035 1 215 14.327 13.343 −6.87% 0.23% x≥1 800 x≥1 100 2.5 1 000 1 055 10.394 9.908 −4.68% 0.21% x≥1 400 x≥900 3.5 1 000 1 005 8.046 7.800 −3.06% 0.19% x≥1 200 x≥900 4.5 960 1 000 6.549 6.404 −2.21% 0.18% x≥1 100 x≥800
下载: 导出CSV
-
[1] 国家环保局. 大气污染物综合排放标准: GB 16297-1996[S]. 北京: 中国环境科学出版社, 1996. [2] ZHU Y, TONG Q L, YAN X X, et al. Development of an uncertain Gaussian diffusion model with its application to production-emission system management in coal-dependent city- a case study of Yulin, China[J]. Energy Procedia, 2019, 158: 3253-3258. doi: 10.1016/j.egypro.2019.01.993 [3] OZA R B, INDUMATI S P, PURANIK V D, et al. Simplified approach for reconstructing the atmospheric source term for Fukushima Daiichi nuclear power plant accident using scanty meteorological data[J]. Annals of Nuclear Energy, 2013, 58: 95-101. doi: 10.1016/j.anucene.2013.03.016 [4] EBRAHIMI M, JAHANGIRIAN A. New analytical formulations for calculation of dispersion parameters of Gaussian model using parallel CFD[J]. Environmental Fluid Mechanics, 2013, 13(2): 125-144. doi: 10.1007/s10652-012-9260-5 [5] MOK K M, MIRANDA A I, LEONG K U, et al. A Gaussian puff model with optimal interpolation for air pollution modelling assessment[J]. Environment and Pollution, 2008, 35: 111-137. [6] 程穆阳. 高斯模型在中小城市多点源大气扩散模拟中的应用研究[D]. 哈尔滨: 哈尔滨师范大学, 2020. [7] 朱玲. 大气污染物排放监测中最低等效排气筒计算规律研究[J]. 环境监控与预警, 2014, 6(2): 30-31. [8] 仇石. 关于等效排气筒高度计算问题的讨论[J]. 中国西部科技, 2014, 13(7): 66-67. doi: 10.3969/j.issn.1671-6396.2014.07.029 [9] 岳千亮. 关于等效排气筒在环保工作中的应用研究[J]. 环境科学与管理, 2013, 38(11): 134-137. doi: 10.3969/j.issn.1673-1212.2013.11.031 [10] 臧传利, 丁峰, 徐玉凤, 等. 大气估算模式AERSCREEN、SCREEN3气体扩散规律简析[J]. 绿色科技, 2018(18): 85-89. doi: 10.16663/j.cnki.lskj.2018.18.031 [11] 李勇, 李一平, 陈德强. 环境影响评价[J]. 南京:河海大学出版社, 2012: 79-81. [12] 伯鑫, 傅银银, 丁峰, 等. 新一代大气污染估算模式AERSCREEN对比分析研究[J]. 环境工程, 2012, 30(5): 71-76,99. doi: 10.13205/j.hjgc.2012.05.034 [13] 王向东, 董秀明. 多烟囱排放大气环境影响评价工作等级探讨[J]. 电力科技与环保, 2012, 28(04): 5-7. doi: 10.3969/j.issn.1674-8069.2012.04.002 [14] 王英伟, 孙雪. 有风条件下点源高斯模式的参数敏感性分析[J]. 环境科学与管理, 2008, 33(10): 178-180. doi: 10.3969/j.issn.1673-1212.2008.10.049 [15] 张艳君. 工业点源参数对污染物最大落地浓度的影响[J]. 广州化工, 2016, 44(10): 172-174. doi: 10.3969/j.issn.1001-9677.2016.10.062 [16] 徐晓波. 关中地区点源大气污染物扩散数值模拟[J]. 环境保护科学, 2018, 44(3): 98-101. doi: 10.16803/j.cnki.issn.1004-6216.2018.03.016 [17] 杨洪斌, 张云海, 李克非, 等. 估算模式AERSCREEN的参数敏感性研究[J]. 气象与环境学报, 2019, 35(6): 126-131. [18] 李冰晶, 仝纪龙, 潘峰, 等. 高斯烟团模型在石化类项目大气环境风险评价中的应用[J]. 环境工程, 2013, 31(3): 139-143. [19] 丁峰, 李时蓓, 邢可佳. 烟塔合一项目烟气抬升影响因素分析[J]. 环境工程技术学报, 2011, 1(2): 173-180. doi: 10.3969/j.issn.1674-991X.2011.02.029 [20] ISSAKHOV A A, BAITUREYEVA A R. Modeling of a passive scalar transport from thermal power plants to atmospheric boundary layer[J]. International Journal of Environmental Science and Technology, 2019, 16(8): 4375-4392. doi: 10.1007/s13762-019-02273-y [21] 马学礼, 党立晨, 张仁锋, 等. 不同排放标准下的燃煤电厂烟囱高度与落地浓度关系研究[J]. 环境科学与管理, 2016, 41(11): 23-27. doi: 10.3969/j.issn.1673-1212.2016.11.006 [22] 刘玉彻, 杨洪斌, 汪宏宇, 等. 冷却塔烟气抬升高度及污染物浓度变化[J]. 气象与环境学报, 2010, 26(1): 40-44. doi: 10.3969/j.issn.1673-503X.2010.01.009 [23] 吴声浩, 易海涛. 大气扩散模型计算结果析疑[J]. 环境工程, 2013, 31(1): 103-107. [24] 杨洪斌, 张云海, 邹旭东, 等. 烟塔合一排烟方式中下洗过程的浓度分布[J]. 气象与环境学报, 2018, 34(5): 156-162. doi: 10.3969/j.issn.1673-503X.2018.05.020 [25] 刘玉彻, 杨洪斌, 梁刚. 气象条件对烟囱污染物影响的模拟研究[J]. 气象与环境学报, 2008, 24(1): 18-21. doi: 10.3969/j.issn.1673-503X.2008.01.005 [26] 生态环境部. 环境影响评价技术导则大气环境: HJ2.2-2018[S]. 北京: 中国环境出版社, 2018. [27] 黄美芬. AERSCREEN大气估算模式不同参数对NO2估算结果的影响[J]. 化学工程与装备, 2020(10): 273-276. [28] 孙爽. AERSCREEN大气污染估算模式在复杂地形条件下的应用研究[J]. 环境影响评价, 2017, 39(6): 47-51. -
点击查看大图
计量
- 文章访问数: 4709
- HTML全文浏览数: 4709
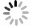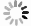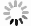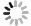
- PDF下载数: 48
- 施引文献: 0
