图1为压裂低渗场地注入-抽提协同强化修复药剂输运的模型简图。如图所示，简化的水力裂缝贯穿整个场地，注入井和抽提井的井筛中心位于裂缝位置，并以等间距L排列。场地的深度为H，裂缝的孔径为b。坐标原点位于研究区域的左下角，x轴与裂缝平行，z轴与裂缝垂直。由于注入井与抽提井是周期等距排列，因此形成注-抽周期对称单元，如图1虚线框所示。为了降低计算量和简化模型，本研究仅探究周期对称单元内的修复药剂的运移情况。考虑对流、扩散、吸附和降解过程，修复药剂在裂缝和土壤中的运移控制方程见式(1)。

式中：下标i = m表示土壤基质，i = f表示水力裂缝；C是修复药剂的浓度，M·L⁻³；t是时间，T；λ是一阶降解速率，T⁻¹；v是达西速度场，L·T⁻¹；$R = 1+\rho {K_d}/\theta $是阻滞因子，θ是孔隙率；K_d是吸附平衡系数，L³·M⁻¹；ρ是土壤密度，M·L⁻³。

D是水动力弥散系数张量，量纲为L²·T⁻¹，计算方法见式(2)~式(4)。

式中：D_e是扩散系数；τ是迂曲因子；E是单位矩阵；D_d是弥散系数；α_L是x方向弥散率，α_T是z方向弥散率，T⁻¹。

修复药剂注入过程中的渗流场由达西定律，见式(5)~式(6)。

式中：ρ_w是流体的密度，M·L⁻³；Q_m是流场的源或汇项；K是介质渗透率，L⁻²；g是重力加速度，L⁻²·T⁻¹；μ是流体粘度，M·L⁻¹·T⁻¹。

在氧化药剂注入之前，场地是完全饱和度，裂缝中和土壤基质中无氧化药剂存在，因此浓度初始条件和压力初始条件见式(7)~式(9)。

在氧化药剂注入过程中，1) 井筛位置的药剂浓度等于搅拌罐中药剂浓度C₀，抽提井位置的出流通量取决于出口的流速和出口位置的药剂浓度； 2) 假设场地修复过程注入井和抽提井位置形成对称的注入和抽提流场，因此出井筛外，其上下位置均为Neumann边界； (3) 注入和抽提过程中均采用恒定压力控制。

式中：p_in和p_ex分别是注入和抽提压力，Pa；H和L分别是计算土层的高度和宽度，L；η是注入和抽提井的筛孔范围，L；b是水力裂缝的孔径，L。修复场地的上边界是地面，下边界设置为不透水层，因此均为无通量边界。

裂缝与土壤基质界面满足浓度连续和通量连续条件，可知。

由式(5~6)可以看出，渗流场主要取决于场地的渗透率和压力，因此在模拟场地异质性时，渗透率场的异质性分布能够很大程度反映场地空间变异特征。半变异函数通常用于描述渗透率在空间上的变异性或相关性。它通过计算不同位置对之间的半变异值来反映样本点之间的空间相关性程度。半变异函数可以表示为式(22)。

式中：σ² 是方差；h是观测点之间的距离；n是块金常数。ρ (h) 是自相关函数，经典的自相关函数包括高斯模型、指数模型、球状模型等。高斯型自相关函数和协方差函数可以表示为式(23~24)。

式中：s是用于调整模型表现的缩放因子；l是相关长度，表征随机场的空间相关性在空间距离上的衰减程度。指数型自相关函数和协方差函数可以表示为式(25~26)。

值得注意的是本研究提到的半变异函数或自相关函数均为弱平稳形式，即假设随机场的均值和方差在整个空间区域内保持不变，协方差函数只与空间距离相关，而与具体的位置无关。换句话说，弱平稳假设允许随机场的统计特性随着空间位置的变化而发生改变，但只要空间距离相同，协方差函数就保持不变。一般来说，弱平稳假设提供了更灵活的建模方式，适用于更多实际场景的数据分析和预测。另一方面，从式(23~24)和式(25~26)可知，指数模型假设半变异值与距离之间呈指数衰减的关系，适用于具有快速减少的空间相关性的情况，而高斯模型假设半变异值与距离之间呈高斯分布的关系，适用于具有光滑且对称的空间相关性的情况。因此，指数模型更适应于描述渗透率的空间变异性，将用于本研究的随机渗透率场的生成。

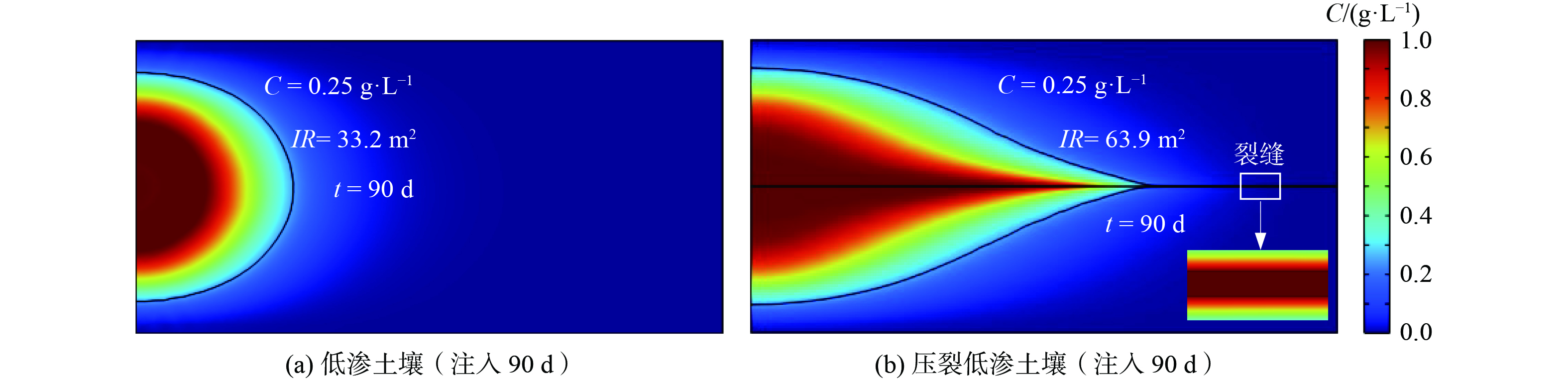
由图1可知，对于一个注-抽周期单元，注入井和抽提井的中轴线可作为对称边界处理，井筛位于边界中间部位，修复药剂在压力的作用下从注入井筛进入土层，然后在注-抽形成稳定渗流场的作用下运移至抽提井。图2显示了低渗场地和压裂后低渗场地中修复药剂注入90 d后的浓度分布情况。相关参数见表1。可以看出，水力裂缝的存在显著增大了修复药剂的运移范围。一般而言，修复药剂的注入效果可通过影范围IR表征，计算如下。

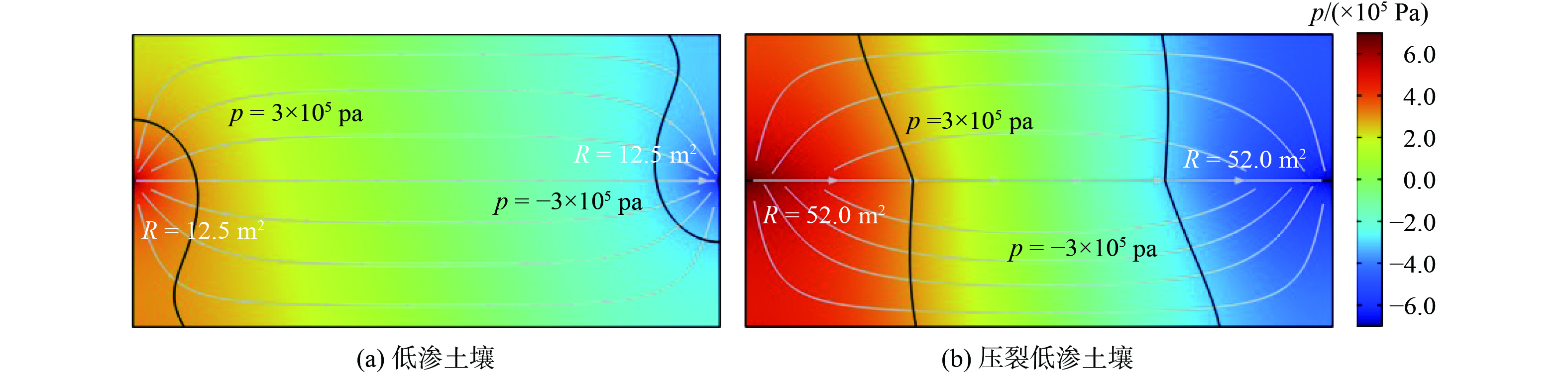
如图2(a)和2(b)所示，以0.25 g·L⁻¹轮廓线为例，相同条件下低渗场地注入修复药剂90 d的影响范围是33.2 m²，而压裂后形成1 cm孔径的水力裂缝后，影响面积为63.9 m²，提高了92.5%。这是由于裂缝的高导流能力在低渗场地中形成了优渗通道，如图2(b)中的子图，裂缝浓度远远高于周围土壤基质中的药剂浓度。另一方面，由于裂缝的高渗特性，也改变土壤中的压力分布。图3显示了低渗场地和压裂场地中，在注入和抽提作用下，场地水压的分布特征。以300 kPa轮廓线为例，低渗场地中压力的影响范围是12.5 m²，而对于压裂场地，压力的影响范围提高到了52 m²，这说明水力裂缝可作为低阻力通道，显著提高注入-抽提压力的有效作用范围。

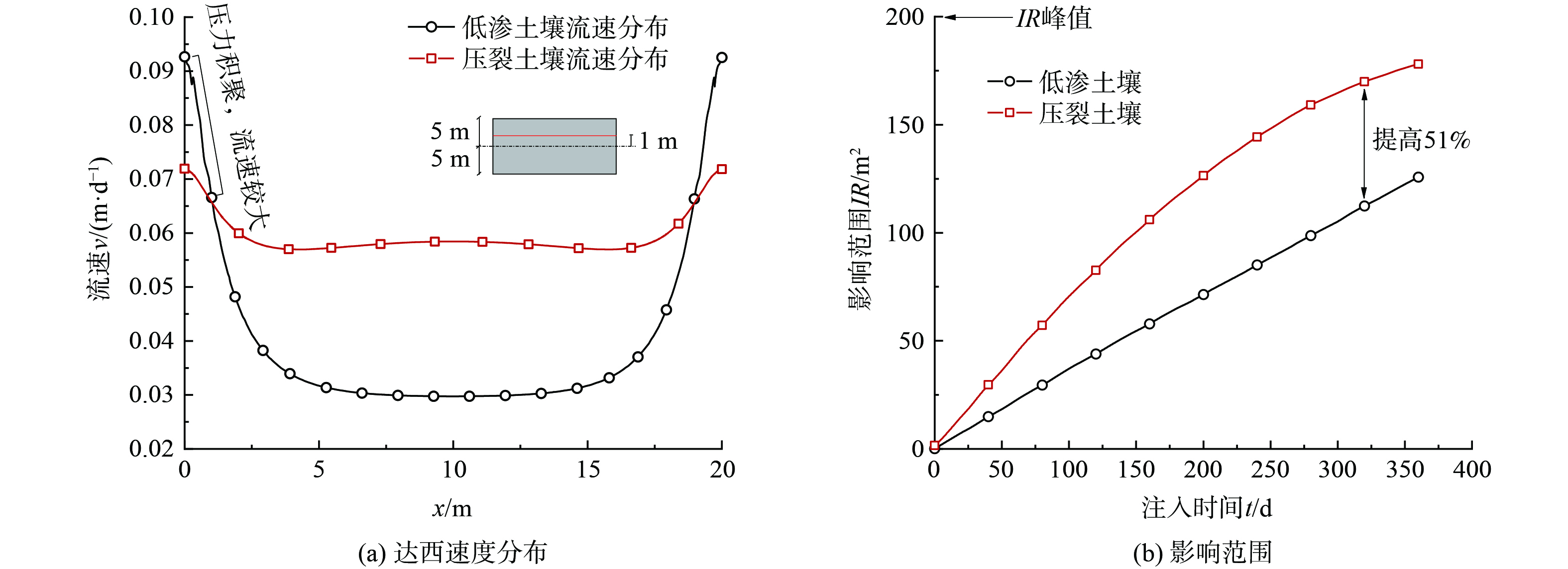
根据达西定律可知，土壤基质中压力的增大会提高对流速率。如图4(a)中对比了低渗场地中轴线上方1 m位置的流速分布。注意裂缝周围1 m位置的药剂浓度是衡量裂缝强化传质的关键参考位置，因为当距离超过1 m后浓度会迅速衰减并显著低于所需浓度。可以看出，低渗场地中，在注入井和抽提井附近3 m以内的位置，由于压力积聚 (图3(a)) ，流速显著高于压裂场地，随后流速迅速衰减至0.03 m·d⁻¹。而对于压裂场地，由于裂缝的低阻力特性，有效促进了压力的传播，因此井附近的流速相对无压裂场地稍低，且随远离井筛距离的增大，流速衰减的幅度明显减小。整体上，低渗土壤水力压裂后，土壤基质中流速提高了近2倍。此外，图4(b)还评估了两种不同工况下修复药剂影响范围的时变特征。可以看出，压裂后修复药剂影响范围始终高于无裂缝的低渗工况。此外，压裂场景中影响范围的增速在后期有降低的趋势。这是由于研究域的尺寸为20 m×10 m，因此影响范围的峰值为200 m²，当修复药剂的影响范围接近该峰值时，药剂会向抽提井收敛，因此速率降低。整体上，当药剂注入时间为90 d时，孔径为1 cm的单裂隙对低渗场地中修复药剂影响范围提升92.5%，当注入320 d时，影响范围提高了50%左右。

大多数的模型均将土壤简化为均质连续模型，然后现实中土壤具有显著的空间变异性，包括土壤密度、土壤矿物成分、孔隙率和渗透率等。在污染场地修复过程中，渗透率对修复药剂和污染物的运移影响最为显著。因此，本节主要研究注入-抽提条件下，渗透率的空间变异性对修复药剂运移和分布的影响。

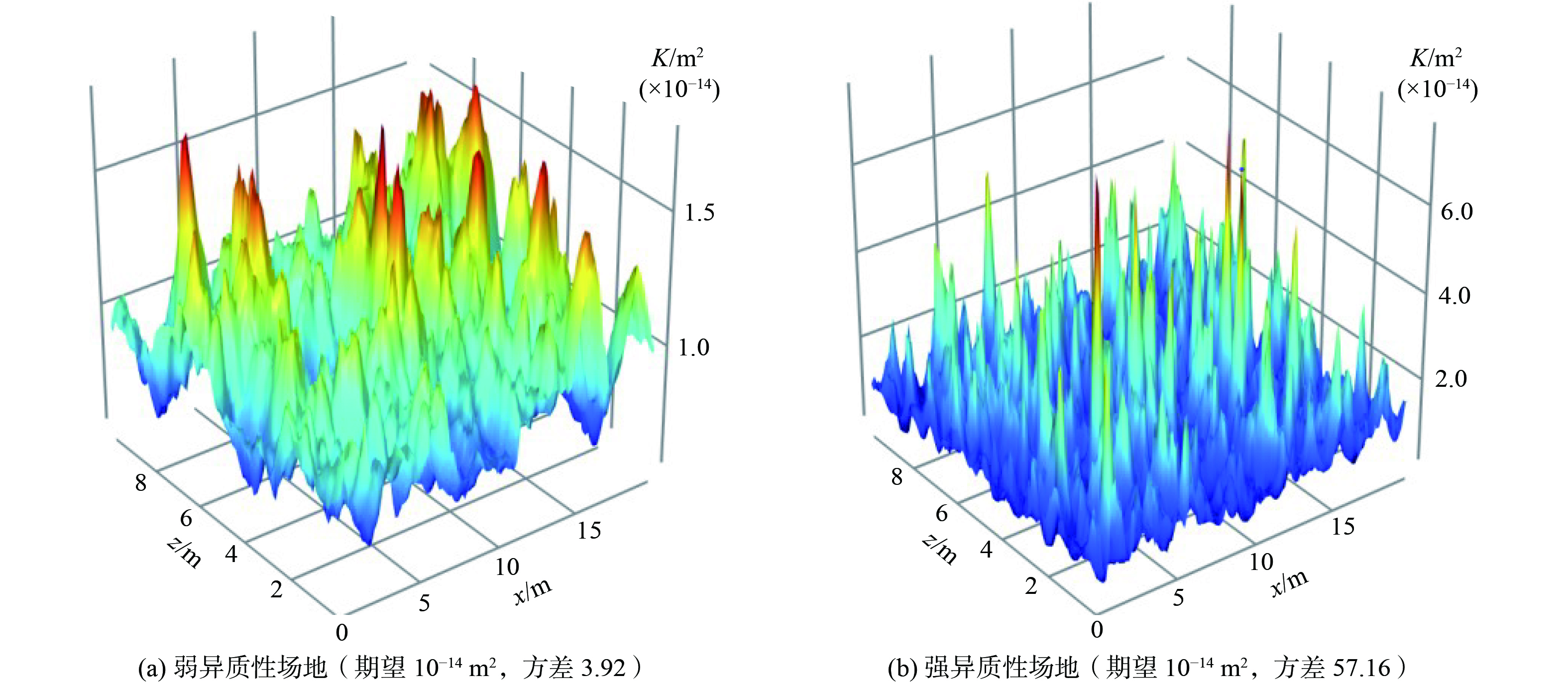
图5显示了结合式(22)和式(25~26)通过python程序生成的随机渗透率场。生成随机渗透率K场后，通过卷积运算对随机场进行平滑处理以消除不连续性或间断点。这里使用的卷积核是一个均匀分布的矩阵，所有的元素值都相等，且元素之和等于1。离散数据集的卷积运算可表示如下。

式中：i和j是随机K场的数据位置；m和n是卷积矩阵中的元素位置；M和N是卷积核的尺寸，尺寸越大，平滑效果越好。当M=N时，卷积核为正方形，可以确保卷积操作在所有方向上的效果是一致的，这正是本节使用的方法。对于低渗场地，10 mD (=1×10⁻¹⁴ m²) 是本研究使用的渗透率，首先使用地统计法对logK进行随机场生成，期望为1，方差为0.5。通过0.5和1.5尺寸的卷积核对生成的随机场进行平滑处理，然后换算得到随机渗透率K场。图5(a)是卷积核尺寸为1.5平滑处理后低异质性随机K场的分布特征，期望为1×10⁻¹⁴ m²，方差是3.92。图5(b)是卷积核尺寸为0.5平滑处理后强异质性随机K场的分布特征，期望为1×10⁻¹⁴ m²，方差是57.16。

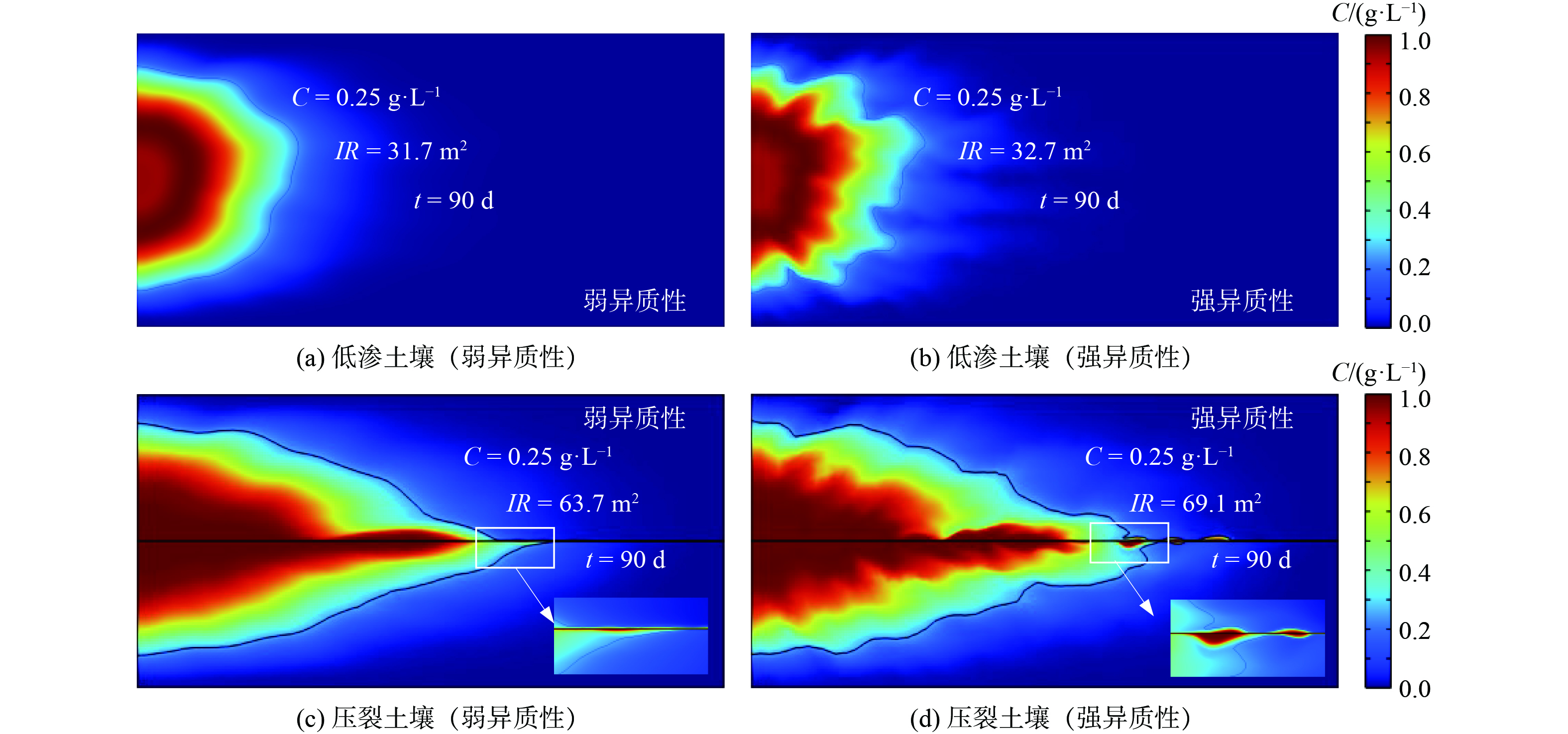
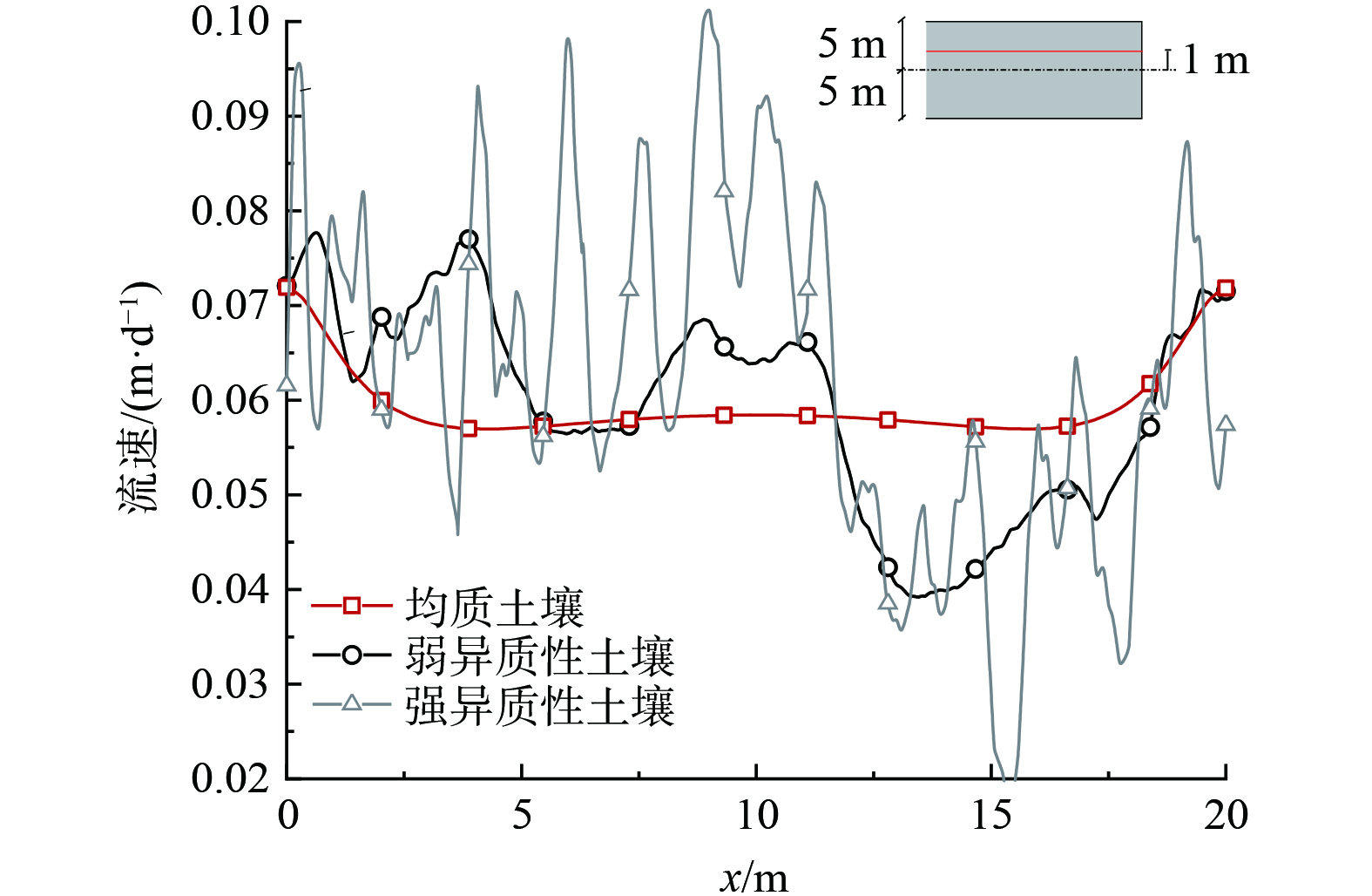
通过将生成的随机K场数据导入COMSOL Multiphysics 6.0，研究修复药剂在注入-抽提作用下的运移域分布特征。模型参数除K值外均与表1中的参数相同。图6显示了未压裂 (a和b) 和压裂条件下 (c和d) ，弱异质场地和强异质场地中修复药剂注入90 d后的分布特征。与均质相比 (图2) ，图6(a)和图6(c)中的修复药剂分布呈现明显的差异性分布，且0.25 g·L⁻¹的轮廓线也不再是光滑的曲线。而对于强异质性场地而言 (图6(b)和图6(d)) ，浓度分布的波动变得更加显著，0.25 g·L⁻¹的轮廓线也更加粗糙，且局部出现浓度聚集。对于不同异质性条件，相比于低渗土壤 (图6(a)和图6(b)) ，压裂后 (图6(c)和图6(d)) 药剂注入90 d的影响范围显著提高，与图2类似。渗透率K场的空间变异性对渗流场的影响如图7所示。与均质场地相比，异质性场地的流速分布出现了明显的波动，且异质性越大波动越显著。值得注意的是局部流速的变化会影响修复药剂与土壤颗粒的相互作用，如吸附-解吸过程，较高的流速会削弱这种传质过程，因此可能导致修复药剂吸附浓度分布的异质性。

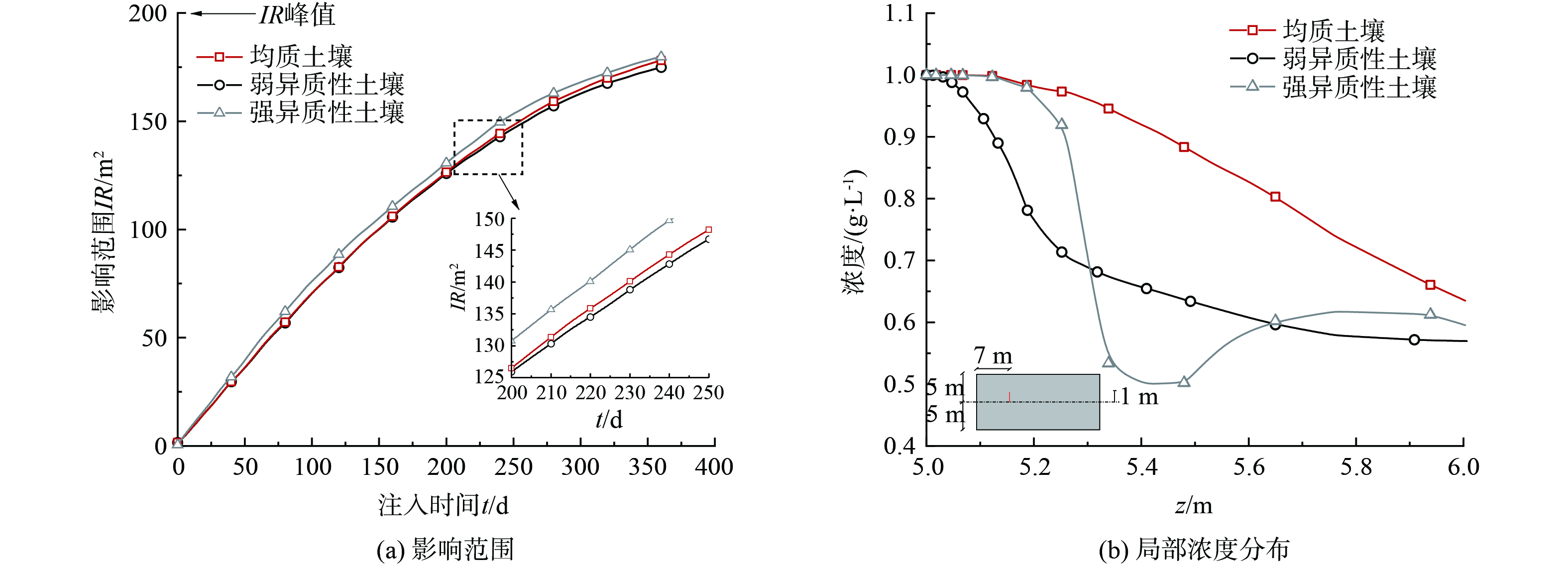
图8(a)对比了均质场地、弱异质性场地和强异质性场地中修复药剂影响范围的时变特征。可以发现，不同场地条件下修复药剂的影响范围的变化趋势无明显差异，且不同注入时间的影响范围IR差异也并不显著。以注入90 d为例 (图2(b)、6(a)、6(b)) ，均质场地、弱异质性场地和强异质性场地的影响范围分别是63.9、63.7和69.1 m²。这说明均质简化模型对于影响范围的评估具有一定的可靠性。然而应当注意的是，异质性会导致修复药剂的分布产生显著的空间变异性。图8(b)显示了连续注入90 d，距离注入井7 m位置土壤中修复药剂的浓度分布。可以看出，与均质场地相比，弱异质性场地的浓度较低。而对于强异质性场地而言，浓度波动较大，可能造成修复药剂出现局部过量或不足的情况，因此造成修复药剂的浪费或污染物修复效率不高的弊端。例如，假设该污染场地为达到修复目标药剂浓度至少应为0.7 g·L⁻¹，那么图8(b)中z = 5.4 m位置处，弱异质性场地药剂缺失率为7.14%，而对于强异质性场地药剂缺失率达28.57%。总而言之，在污染场地修复的过程中，在评估污染物分布和修复药剂的用量时应考虑场地的异质性。需要说明的是，为了提高计算效率本文生成渗透率随机场使用了较小的方差 (σ² = 0.5) ，然而实际工程中地质特性统计学方差同样存在较大的情况，因此未来需要更加深入的研究。此外，由于篇幅有限，本研究没有详细研究裂缝性质 (如裂缝迂曲形态，裂缝孔径、裂缝表面粗糙度) 对药剂输运的影响，为更加全面和深入理解裂缝影响机制，未来工作中这些因素的详细分析是十分必要的。

1) 与低渗场地相比，水力裂缝可通过增强场地压力传递能力提高渗流速率，从而强化药剂输运。此外，裂缝可作为优渗通道优先形成药剂线源然后与周围土壤基质通过质量交换强化药剂输运。例如低渗污染场地中水力压裂形成孔径为1 cm的单裂隙条件下，药剂连续注入90 d时影响范围提高92%；药剂连续注入320 d时，影响范围提高50%左右。

2) 与均质场地相比，异质性场地中修复药剂出现显著的浓度波动，且异质性越强，浓度差异性越明显，浓度轮廓线越粗糙。此外，异质性还显著影响场地的渗流场分布，强异质性通常对应达西速度的高波动分布，并潜在地影响土壤的传质过程。

3) 就影响范围的评估而言，均质简化模型与异质性模型 (σ² = 0.5) 的差异并不明显，但是在评估污染物的分布特征和修复药剂的用量时需要着重考虑异质性的影响，因为异质性场地会出现污染物或修复药剂的局部累积。从业者在指定修复方案时如果忽略异质性的影响可能导致修复药剂出现局部过量或不足的情况，因此造成修复药剂的浪费或污染物修复效率不及预期。例如，当假设该污染场地为达到修复目标药剂浓度至少为0.7 g·L⁻¹时，弱异质性场地特定位置的修复药剂缺失率为7.14%，而对于强异质性场地药剂缺失率达28.57%。